Oct
10
Creo que siempre, buscaremos algunas respuestas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (2)
Comments (2)

Imaginemos una mente tan inteligente que, en todo instante, pudiera tener conocimiento de todas las fuerzas que controlan la Naturaleza y también, de las condiciones en que se encuentran en cada instante todas las entidades e consta el Cosmos “infinito”. Si esta mente tuviera una inteligencia suficiente para analizar todos esos datos, podría abarcar con una sola fórmula los movimientos de los cuerpos de mayor tamaño del universo y, los de los átomos más ligeros; para ella nada sería incierto; el futuro y el pasado estarían ambos ante sus ojos, no habría secretos ni misterios para ella y, si eso fuese posible…¿sería una mente feliz?

Elequivalente de esa mente poderosa podría ser un superordenador que conocería las posiciones y las velocidades de todaslas partículas del universo, y pudiera utilizar las leyes de Newton y las que describen las fuerzas de la Naturaleza (como la Gravedad y el electromagnetismo), no solo para predecir la trayectoria futura de cada partícula, sino para averiguar toda la historia de su procedencia -porque en las leyes de Newton no hay nada que revele la dirección del tiempo y funcionan de la misma manera si éste transcurre en sentido contrario, como podemos ver fácilmente si nos imaginamos el proceso inverso del hipotético choque entre dos mundos, o, si invertimos los mocimientos orbital de todos los planetas del Sistema solar-.
No exioste flecha del tiempo en las leyes de Newton y, según Laplace y muchos otros, estas leyes parecen describir un mundo completamente determinista en el cual el pasado y el futuro están fijados de una manera rígida y no existe lugar para el libre Albedrío.
Lo que ninguno de estos científicos parece haber observado es que el argumento fundamental se desploma si, en cualquier momento y lugar del universo, se produce una colisión simultánea entre tres partículas -aunque la valoración si esto sería suficiente para restablecer el libre albedrío es una cuestión cuya discusión prefiero dejar a los filósofos.
Según las leyes de Newton, las colisiones entre pares de objetos son perfectamente reversibles. La imagen resulta igualmente plausuble con independencia de cómo tracemos la “Flecha del Tiempo”.
Este mismo problema relativo al Tiempo se planteó a partir de uno de los mayores triunfos de la física del siglo XIX: la investigación de la naturaleza de la luz y de otras formas de radiación electromagnética, que tuvo su momento culminante en la obra del escocés James Clerk Maxwell. La explicación dada por Maxwell sobre la radiación electromagnética se basaba en la obra de Michael Faraday que fue el primero en proponer la existencia de un “campo” eléctrico y magnético que surgían en torno a imanes y objetos que poseyeran carga eléctrica.
Fue Faraday el que propuso que la luz podía estar producida por algún tipo de vibración de las lineas de fuerzas asociadas con umánes y partículas cargadas, que vibrarían como lo hacen las cuerdas de un violún al ser pulsadas. Faraday, un esencial experimentador, carecía de los conocimientos necesarios para formular las ecuaciones que expresaran sus ideas. La llegada de Maxwell solucionó aquel problema y, viendo con diáfana claridad todo lo que Faraday había hecho y lo que sus propuestas implicaban, desarrollo el trabajo que termino en 1860 y, mediante cuatro ecuciones vectoriales, demostró al mundo que, todos los fenómenos eléctricos y magnéticos conocidos en aquella época, incluído el comportamiento de la luz, podían describirse mediante su conjunto de su cuatro ecuaciones. Estas ecucianes eran para las radiaciones y para los campos electromagnéticos lo que las leyes de Newton para la materia sólida.
Entre los dos, Newton y Maxwell aportaron el conjunto de herramientas matemáticas para controlar todo lo que la Física conocía a mediados del siglo XIX. Por otra parte, lo más maravilloso de las ecuaciones de Maxwell era que, sin que se hubiera pedido, proporcionaba una descripción de la luz -las ecuciones se crearon para describir otros fenómenos electromagnéticos, pero incluían en sí misma una solución que describía las ondas electromagnéticas que se desplazaban por el espacio as cierta velocidad-. Esta velocidad es, exactamente, la velocidad de la luz, es decir 299.792,458 k/s que, ya había quedado bien determinada en la década de 1860 y pronto se podría medir con una precisión aún mayor que nos llevó a la que hoy conocemos y que arriba dejo reseñada.
¿Qué es lo que dicen en conjunto? Son la descripción del campo electromagnético: el campo eléctrico, el campo magnético, su origen, comportamiento y relación entre ellos, incluyendo las ondas electromagnéticas como la luz. Básicamente, con estas ecuaciones es posible saber cómo va ser y cómo va a comportarse el campo electromagnético en una región determinada, a partir de las cosas que hay allí. La contrapartida, es decir, qué le pasa a las cosas que hay allí a partir del campo electromagnético, está descrita por la fuerza de Lorentz, de la que no vamos a hablar hoy. El conjunto de estas ecuaciones describe cosas como la corriente eléctrica, los imanes, los rayos, la electricidad estática, la luz, las microondas, la radio… vamos, son un filón.
Hay un par de cosas más que es conveniente saber sobre estas cuatro ecuaciones. La primera es que, expresadas matemáticamente o en lenguaje común, representan leyes físicas. No tienen demostración, sino que juntas constituyen una teoría que ha sido verificada experimentalmente. Dicho de otro modo, si alguien realizase experimentos que nos demuestren que estas ecuaciones son una estupidez, las tiraríamos a la basura y a otra cosa, mariposa. Sin embargo, esto no ha sucedido así ni es probable que suceda: más bien hemos ido comprobando aspectos en los que se acercan a la realidad pero fallan ligeramente, de modo que las hemos ido modificando para tener en cuenta cosas como la cuántica o la relatividad. Eso sí, el espíritu y el significado último siguen siendo básicamente los mismos.

Ampère, Coulomb, Gauss, Ørsted, Faraday (escondido, su timidez no le deja asomarse).
El segundo detalle a tener en cuenta es que, como veremos en el siguiente epígrafe, las ecuaciones originales no eran cuatro y las que usamos hoy en día no son exactamente las mismas que propuso James Clerk Maxwell. El bueno de James utilizó algunas otras magnitudes diferentes, y unas cuantas ecuaciones más, mientras que fue Oliver Heaviside quien hizo un pulido, remodelación y lavado de cara que nos proporcionó lo que ves arriba y sus otros equivalentes matemáticos.
Es más, de las cuatro ecuaciones de arriba, la única en la que Maxwell hizo una contribución concreta y novedosa es la última, de modo que cada una de las cuatro ecuaciones llevan el nombre de otro científico –quien propuso cada una–, con el propio Maxwell compartiendo honor en esa última. Puede que al leer esto hagas una mueca de desdén a este escocés genial, pero creo que sería una equivocación: a menudo, el genio está en sintetizar, no en crear. Como veremos en un momento, muchos científicos habían ido descubriendo pinceladas del comportamiento eléctrico y magnético de las cosas, pero eran eso, retazos. Hacía falta un auténtico genio para relacionar unas ideas con otras y mirar las cosas como un todo, y ese genio fue Maxwell. Pero veamos, brevemente, cómo sucedió todo.






La expresión “Flecha del tiempo” fue acuñada en el año 1927 por el astrónomo británico Arthur Eddington, quien la usó para distinguir una dirección en el tiempo en un universo relativista de cuatro dimensiones. En 1928, Eddington publicó un libro llamado “The Nature of the Physical World”, en el que utilizó varias veces esa expresión. En el libro, el autor escribió:
Dibujemos una flecha del tiempo arbitrariamente. Si al seguir su curso encontramos más y más elementos aleatorios en el estado del universo, en tal caso la flecha está apuntando al futuro; si, por el contrario, el elemento aleatorio disminuye, la flecha apuntará al pasado. He aquí la única distinción admitida por la física. Esto se sigue necesariamente de nuestra argumentación principal: la introducción de aleatoriedad es la única cosa que no puede ser deshecha. Emplearé la expresión “flecha del tiempo” para describir esta propiedad unidireccional del tiempo que no tiene su par en el espacio.
A pesar de que Eddington se refiere a la dirección del tiempo desde un punto de vista netamente relacionado con la física, nuestra experiencia diaria no puede escapar a su razonamiento. Supongamos observamos una copa de cristal que cae de una mesa, y al llegar al piso se rompe en mil pedazos que se esparcen por varios metros cuadrados del piso. Nuestra experiencia indica que la “copa entera” pertenece al pasado, y que la dirección en que fluye el tiempo es la contiene en su futuro una copa hecha añicos. Si alguien filmase ese evento y nos proyectase la película en sentido inverso, cuando viésemos un montón de trozos de vidrio que salen disparados en la misma dirección, chocan y se funden creando una copa que salta hacia arriba de la mesa, sabríamos de inmediato que algo está mal. Ese tipo de acontecimiento -en general- no tiene lugar en nuestro universo.
Podríamos estar hablando de conceptos aparentemente inconexos y, no tendríamos tiempo, durante todo el día, para finalizar lo que nos dictan los pensamientos que acuden en tropel a nuestras mentes, así que, lo dejaremos aquí por hoy y,lo que hemos tratado quizá, con userte, haga pensar a alguno de ustedes lectores que, quisiera profundizar más sobre los conceptos tratados.
emilio silvera
Oct
7
¡Los Físicos! Algunas veces poetas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (2)
Comments (2)
Masa-Energía-Materia-Luz: Todo la misma cosa:
¡El Universo!
Un apunte que sea un… Preludio a la relatividad
-Las ecuaciones de Lorentz-Fitzgerald-
En 1893, el físico irlandés George Francis FitzGerald emitió una hipótesis para explicar los resultados negativos del experimento conocido de Michelson-Morley. Adujo que toda materia se contrae en la dirección del movimiento, y que esa contracción es directamente proporcional al ritmo (velocidad) del movimiento.
Según tal interpretación, el interferómetro se quedaba corto en la dirección del “verdadero” movimiento terrestre, y lo hacía precisamente en una cantidad que compensaba con toda exactitud la diferencia de distancias que debería recorrer el rayo luminoso. Por añadidura, todos los aparatos medidores imaginables, incluyendo los órganos sensoriales humanos, experimentarían ese mismo fenómeno.
Oct
1
La Fisica, ¡que maravilla!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (9)
Comments (9)
En el mundo de los seres vivos, la escala o tamaño crea importantes diferencias. En muchos aspectos, la anatomía de un ratón es una copia de la de un elefante, pero mientras que un ratón puede trepar por una pared prácticamente vertical sin mucha dificultad (y se puede caer desde una altura varias veces mayor que su propio tamaño sin hacerse daño), un elefante no sería capaz de realizar tal hazaña. Con bastante generalidad se puede afirmar que los efectos de la gravedad son menos importantes cuanto menores sean los objetos que consideremos (sean vivos o inanimados).

Cuando llegamos a los seres unicelulares, se ve que para ellos no hay distinción entre arriba y abajo. Para ellos, la tensión superficial del agua es mucho más importante que la fuerza de la gravedad a esa escala.
La tensión superficial es una consecuencia de que todas las moléculas y los átomos se atraen unos a otros con una fuerza que nosotros llamamos de Van der Waals. Esta fuerza tiene un alcance muy corto; para ser precisos, diremos que la intensidad de esta fuerza a una distancia r es aproximadamente 1/r7. Esto significa que si se reduce la distancia entre dos átomos a la mitad de la fuerza de Van der Waals con la que se atraen uno a otro se hace 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128 veces más intensa. Cuando los átomos y las moléculas se acercan mucho unos a otros quedan unidos muy fuertemente a través de esta fuerza. El conocimiento de esta fuerza se debe a Johannes Diderik Van der Waals (1837 – 1923) con su tesis sobre la continuidad del estado líquido y gaseoso que le haría famoso, ya que en esa época (1873), la existencia de las moléculas y los átomos no estaba completamente aceptado.
La tensión superficial del agua, es el efecto físico (energía de atracción entre las moléculas) que “endurece” la capa superficial del agua en reposo y permite a algunos insectos, como el mosquito y otros desplazarse por la superficie del agua sin hundirse.

El famoso físico inglés James Clerk Maxwell, que formuló la teoría del electromagnetismo de Faraday, quedó muy impresionado por este trabajo de Van der Waals.
Los tamaños de los seres uniceculares, animales y vegetales, se miden en micrómetros o “micras”, donde 1 micra es 1/1.000 de milímetro, aproximadamente el tamaño de los detalles más pequeños que se pueden observar con un microscopio ordinario. El mundo de los microbios es fascinante, pero no es el objeto de este trabajo, y continuaremos el viaje emprendido hacia las partículas elementales que forman núcleos, átomos, células y materia, así como las fuerzas que intervienen en las interacciones fundamentales del universo y que afecta a todo lo que existe.
Sep
28
Cosas de Física a petición del un Centro Escolar
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (2)
Comments (2)
Acoplamiento espín órbita:
El pequeño cuadrado verde en esta imagen marca el punto cero grados de latitud y 180 º de longitud en la superficie de Mercurio. Este es una de los dos “polos calientes” de Mercurio . El otro es en la latitud 0 ° y 0 ° de longitud. La excéntrica órbita de Mercurio y el acoplamiento espín-órbita se combinan de modo que uno u otro de estos “polos calientes” apunta hacia el Sol cuando Mercurio pasa más cerca del Sol en su órbita, y este se encuentra arriba ya en estos puntos que en cualquier otro lugar del planeta… Pero, lo que quierp decir es que…
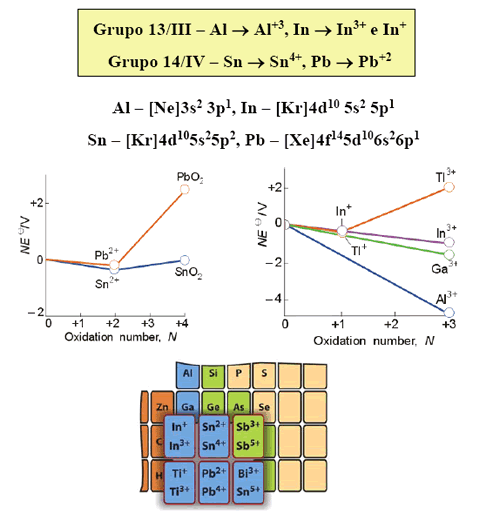
Es Interacción entre el momento angular orbital y el momento angular de espín de una partícula individual, como un electrón. Para los átomnos ligeros, el acoplamiento espín-órbita es pequeño, de manera que los multipletes de los átomos de muchos electrones se describen por el acoplamiento de Russell-Saunders. Para los átomos pesados, el acoplamiento espín-órbita es grande, de forma que los multipletes de los átomos de muchos electrones se describen por el acoplamiento i-i. Para los átomos de tamaño medio las magnitudes de las energías asociadas con el acoplamiento espín-órbita son comparables a las magnitudes de las energías asociadas con la repulsión electrostática entre los electrones, estando los multipletes descritos en este caso por un acoplamiento intermedio. El de espín-órbita es grande en muchos núcleos, particularmente en los nñucleos pesados.
Empezaremos considerando a un electrón girando sobre sí mismo como si fuese un trompo, una imagen que representa una buena simbolización del momento angular de spin de dicha partícula. El mismo electrón además de poseer este momento angular intrínseco posee también otro tipo de momento angular al estar atrapado orbitalmente como parte de un átomo:
Aunque ambos momentos angulares son cosa aparte, aceptemos que poseen la característica de poder acoplarse para dar origen a nuevas líneas en el espectro, las cuales no pueden ser explicadas sin la presunción de ese acoplamiento. Por acoplamiento entendemos la suma de los momentos angulares, orbital y de spin, y dándoles a estas cantidades una cualidad pseudo-vectorial al igual que como se acostumbra a hacerlo en la mecánica clásica, el momento angular total J se define como la suma “vectorial” del momento angular de spin S y el momento angular orbital L:
Todo profesor, casi siempre, se ve en apuros cuando un alumno plantea algunas de las siguientes interrogantes: ¿por qué el mercurio es líquido?, ¿por qué la plata y el oro tienen diferente color?, ¿a qué se debe realmente el efecto del par inerte?, ¿cómo podría explicar la contracción del bloque d o la contracción lantánida? o ¿por qué algunos elementos tienen configuraciones electrónicas aparentemente anómalas? Por no mencionar el acoplamiento espín-orbital y los valores extraños en: los potenciales de ionización, las afinidades electrónicas, los desplazamientos químicos en el RMN, entre otros.
Como todos sabemos, el estudio del comportamiento del electrón en el átomo se lleva a cabo matemáticamente resolviendo la ecuación de Schrödinger que, en algunos textos, se puede encontrar simplificada (ecuación 1a) o más desarrollada (ecuación 1b)
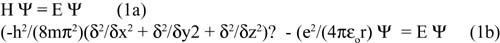
donde h es la constante de Planck, m es la masa del electrón, x, y, z son las coordenadas del electrón, e es la carga del electrón, r es la distancia del electrón al núcleo, εo es la permisividad del vacío, Ψ es la función de onda y E es la energía. La solución de esta ecuación consiste en encontrar valores para ? y E. Al resolver esta ecuación aparecen tres números cuánticos: n, l y m l . No aparece el cuarto número cuántico, el espín, como algunos textos dan a entender erróneamente. En este tratamiento mecánico cuántico -que se encuentra en casi todos los textos de química- se asume que la velocidad del electrón es pequeña comparada con la velocidad de la luz (c ) y que su masa (m) es aproximadamente igual a su masa en reposo (m o ). Esta simplificación, que se conoce como mecánica cuántica no-relativística, es adecuada para explicar muchos parámetros de los elementos químicos más ligeros. Sin embargo, falla al tratar de explicar valores como las distancias y energías de los electrones para los elementos más pesados. Cuando la carga nuclear se incrementa, la atracción de los electrones hacia el núcleo crece, lo que ocasiona que los electrones se muevan a mayor velocidad; en algunos casos, es cercana a la de la luz. Por ello, en los átomos más pesados los electrones internos tienen velocidades muy grandes y se sabe por la teoría de la relatividad, dada por Einstein en 1905, que la masa de cualquier objeto que se mueve se incrementa a medida que aumenta su velocidad. Cuando se toma en cuenta la gran velocidad con la que el electrón realmente se mueve y corrigiendo su masa por las ecuaciones 2 y 3, entramos al campo de la mecánica cuántica relativística y eso fue lo que Dirac desarrolló en el año 1925.
donde Z es el número atómico, v es la velocidad del electrón y m es la masa relativística del electrón.
La ecuación de Dirac para estudiar el comportamiento del electrón en el átomo (ecuación 4) es análoga a la de Schrödinger:1
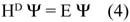
donde HD es el Hamiltoniano de Dirac para muchos electrones.
Por ejemplo, para el mercurio, Z = 80, si aplicamos la ecuación (2) calculamos la velocidad que debe ser aproximadamente 0,58 c (58 % de la velocidad de la luz). Luego por la ecuación (3) calculamos la masa en movimiento que es más o menos 1,23 mo. Conociendo la masa del electrón se puede calcular el radio de Bohr mediante la fórmula 5:
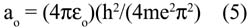
de donde se encuentra que la distancia promedio para el electrón que está en el nivel 6s del mercurio, a o , será un 23 % menor a la correspondiente al valor no-relativístico. En otras palabras, el orbital se comprime un 23 % cuando se toma en cuenta el efecto relativístico. Para el electrón 1s del átomo de hidrógeno los resultados relativísticos indican que su masa es 1.00003 × m o . Se comprime un 3 x10 –5 %, cantidad insignificante al considerar el efecto relativístico.
Como hemos visto, la diferencia de la distancia entre el electrón y el núcleo, así como las energías de los electrones, es pequeña cuando comparamos los valores obtenidos por los efectos relativísticos y los no relativísticos, para los elementos ligeros. Pero esta diferencia aumenta para los elementos pesados, por efecto del incremento de la carga nuclear donde se observa que realmente todos los orbitales s se contraen bastante y también los p.
El espín electrónico fue un término acuñado por Uhlenbeck y Goudsmit 2 en 1925 para explicar la estructura fina del espectro del átomo de hidrógeno (que también explica el resultado del experimento realizado en 1922 por Stern y Gerlach con los átomos de plata) y aplicado al movimiento intrínseco del electrón. Dirac, al realizar el tratamiento matemático aplicando los principios de la mecánica cuántica y la relatividad, encontró que el acoplamiento espín-orbital es un efecto puramente relativístico. Todos los electrones, incluyendo los s, tienen momento angular y no hay distinción entre momento angular orbital y momento angular del espín. Sólo hay un momento J, momento cuántico angular. La interacción espín-orbital divide una capa de un valor dado de l (número cuántico del momento angular) en subcapas con un total de momento angular j = l – ½ y j = l + ½. Por ello los 3 orbitales p son diferentes; ellos forman dos grupos de orbitales p 1/2 y p 3/2. La diferencia de energía entre estas subcapas viene a ser justo la energía espín-orbital. Tras ello, Dirac propuso que el orbital s debe recibir la denominación s 1/2 , que es el momento angular que aparece en las mediciones espectroscópicas. Como s 1/2 y p 1/ 2 tienen la misma dependencia angular, un orbital p 1/2 es de hecho esféricamente simétrico y tiene una menor energía que el p 3/2 . (éste último tiene la forma de una dona). Este desdoblamiento energético de los orbitales es la explicación para la energía de acoplamiento espín-orbital.
Un tratamiento matemático riguroso, que no vamos a desarrollar aquí, concluye que los efectos relativísticos aplicados a los orbitales atómicos son tres:
1. La contracción radial relativística y la disminución (mayor estabilización) energética
de los orbitales s y p.
2. Los electrones en orbitales donde l > 0 (p, d, f, …) sufrirán el conocido desdoblamiento espín-orbital en j = l + s; j = l ± 1/2.
3. Los electrones en orbitales d y f, debido a que serán más eficientemente apantallados por la contracción de las capas s y p, se orientan radialmente hacia fuera y subirán en energía (se desestabilizan). Esto se conoce como efecto relativístico indirecto o de segundo orden.
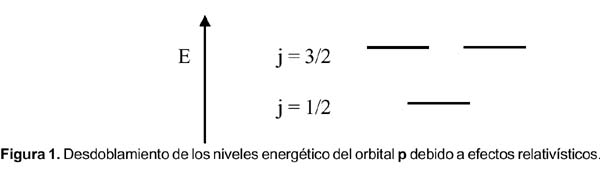
Estos tres efectos son de la misma magnitud y crecen a medida que lo hace Z 2 . Aplicado a un elemento pesado, como el oro (figura 2), da lugar a una distribución energética de los orbitales atómicos diferente a la que aparece en muchos textos de química.
La mecánica cuántica resulta difícil no sólo por las matemáticas, sino también debido a que surgen conceptos que son difíciles de comprender, no sólo por alumnos o profesores sino que escapa a la cotidianidad del ser humano. Por ejemplo, nosotros podemos percibir un gira de 90º, 180º y hasta uno de 360º; sin embargo, el electrón tiene un giro de 720 º ¡ningún ser humano puede percibir semejante giro! La velocidad promedio del electrón 1s del átomo de hidrógeno (Z = 1) es ca. 2 × 10 6 m s -1 ; si considerásemos al electrón como una partícula podríamos verlo orbitando el núcleo 10 15 veces en un segundo. En el caso del electrón 1s del oro (Z = 79) su velocidad promedio es mucho mayor que en el caso anterior ca. 1,6 × 10 8 ms -1 , velocidad cercana a la de la luz, c = 3 × 10 8 ms -1 .
A pesar de la importancia de los efectos relativísticos en la química, muy pocos textos los toman en cuenta o siquiera los mencionan. Una de la excepciones es el libro de Química Inorgánica Descriptiva de Geoff Rayner-Canham.3 A continuación veremos cómo se altera nuestra comprensión de parámetros y conceptos químicos debido a los efectos relativísticos, campo en el cual actualmente se realizan muchos estudios teóricos.
EFECTOS RELATIVÍSTICOS EN LOS ELEMENTOS
1. ¿Qué tiene de particular el mercurio para que este elemento sea líquido a temperatura ambiente?
La configuración electrónica para el mercurio es [Xe]4f 14 5d 10 6s 2 y debido a los efectos relativísticos, los orbitales d y f deben subir en energía (desestabilizarse), mientras que los orbitales s, se acercan más al núcleo y se estabilizan. Un diagrama OM para la molécula Hg 2 , similar al diagrama bien conocido del He 2 , se muestra en la figura 3.
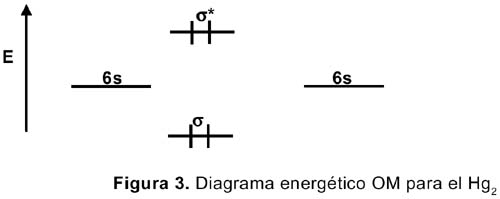
Vemos que los orbitales antienlazantes están poblados lo cual desestabiliza a la molécula diatómica. En fase gas el Hg está formando especies monoméricas. En el caso del vecino que precede al mercurio, el oro, con una configuración [Xe]4f 14 5d 10 6s 1 , formaría una molécula Au 2 estable en fase gas. Los electrones 6s del mercurio, al estar muy establizados en energía, no contribuyen mucho a la formación del enlace Hg-Hg. Lo cual nos lleva a que el enlace mercurio-mercurio debe ser debido a las fuerzas de van der Waals y probablemente a una débil interacción 6p. Ambas fuerzas son muy débiles. Esta es la razón por la cual el enlace Hg-Hg es tan débil. En el caso de los elementos del mismo grupo del Hg, Zn y Cd, los orbitales 4s y 5s, respectivamente, no están tan estabilizados en energía, como en el caso del mercurio.2
Por otro lado, es bien conocido que la especie [Hg-Hg]2+ es muy estable; se conocen muchos compuestos tanto en solución como en fase sólida. Un leve análisis de la configuración electrónica nos revela que esta especie es isoelectrónica al Au 2 que, como ya se mencionó, es estable. También, por efectos relativísticos las distancias Au 2 y Hg 2 2+ son un 16 % más cortas que en el caso de los análogos de plata y cadmio.
Además, la conductividad eléctrica en el Hg es mucho menor que la del Au, ello debido a que los dos electrones 6s están muy localizados y contribuyen muy poco a la banda de conducción.
Beta de Oro
2 ¿Por qué el oro tiene un color diferente a la plata?
Para este caso debemos comparar la distribución energética de los orbitales de valencia de ambos elementos. El color del oro podría deberse a una transición electrónica de un electrón 5d 5/2 al nivel 6s 1/2 (ver figura 2), cuando la luz azul es absorbida. En el caso de la plata la transición deber ser análoga del 4d 5/2 a 5s 1/2 , pero como en el caso del Au (que tiene mayor Z) la diferencia de energía entre los orbitales 6s 1/2 y 5d 5/2 es más pequeña que en el caso 5s 1/2 y 4d 5/2 . Esta última cae dentro del rango del ultravioleta y la del oro en el rango del visible. Sin embargo, la transición, 5d 5/2 a 6s 1/2 está prohibida; por ello, en el caso del átomo de oro debería ser incoloro y no amarillo. Nuestro error está en que hemos debido considerar la teoría de bandas ya que observamos el color amarillo en un bloque sólido de oro, no en un átomo de oro. Y para ello, la teoría de bandas es la apropiada; en ella la diferencia de energía entre las bandas de valencia llenas (esencialmente d) y la banda de conducción (esencialmente s) es 2,4 eV para el oro y 3,7 eV para la plata. La primera cae dentro del rango del visible y la segunda en el ultravioleta. Tal como en el caso anterior, el nivel de cercanía entre las bandas es mayor en el caso del oro, con respecto a la plata, por los efectos relativísticos.
3. ¿Por qué existen valores anómalos en las energía de ionización y la afinidad electrónica?
Es bien conocido el hecho de la variación de la energía de ionización (EI) a lo largo de los elementos del grupo 13 al 18, tal como se muestra en la tabla 1
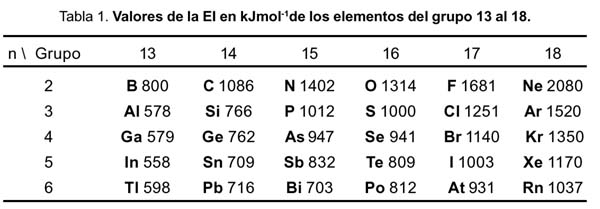
La explicación de estas variaciones se basa en varios hechos: a lo largo de un periodo la carga nuclear se incrementa, a la repulsión electrón-electrón y al apantallamiento incompleto de los electrones. Para los casos donde n = 2, 3, 4 y 5 la explicación, encontrada en los textos, introduce el concepto de repulsión electrón-electrón. La menor repulsión electrón-electrón se logra cuando los espines de los electrones son paralelos ya que cada par de espines paralelos contribuye a una estabilización de intercambio energético del átomo. Por ello, para estos casos, la EI depende del número de pares de espines paralelos que se pierden en la ionización. Por ejemplo, para el caso del nitrógeno, el cambio en el número de espines paralelos al pasar de p 3 a p 2 es de dos, pero para el oxígeno, que cambia de p 4 a p 3 , la variación es cero y se desestabiliza teniendo una menor EI que la del nitrógeno.
Por otro lado, la explicación de las variaciones cuando n = 6 no se encuentra en los textos. La EI del bismuto es menor que la de sus vecinos el plomo y el polonio. Para estos elementos más pesados debemos considerar el efecto relativístico,4 donde el acoplamiento espín-orbital, o sea el momento angular total J, es más importante que la repulsión electrón-electrón. Si los momentos magnéticos debido al espín y al orbital apuntan en direcciones opuestas, se cancelan mutuamente y la interacción es atractiva (el átomo se estabiliza). En el caso que apunten en la misma dirección, la interacción es repulsiva; por consiguiente el átomo se desestabiliza. De la figura 1, el llenado electrónico en el nivel p y para el caso del plomo, bismuto y polonio son: (p 1/2 ) 2 (p 3/2 ) 0 , (p 1/2 ) 2 (p 3/2 ) 1 y (p 1/2 ) 2 (p 3/2 ) 2 , respectivamente.
Por ello, la EI del bismuto es menor que la del plomo, ya que el electrón del primero ocupa un nivel desestabilizado en energía p 3/2 y del plomo uno establizado p 1/2 . La EI del polonio es mayor que la del bismuto por el efecto del incremento de la carga nuclear efectiva.
En las tablas de las energías de ionización podemos observar una “anomalía”. Los valores de la primera y segunda energía de ionización son para la plata 0,73 y 2,07 MJ/mol y para el oro 0,89 y 1,98. La tendencia general es que la EI disminuya al descender en un grupo, sin embargo, esto no ocurre. Para resolver esta interrogante tendríamos que calcular el valor de las energías de los orbitales de valencia del oro y de la plata. Se puede hacer de una manera indirecta a través de cálculos relativísticos de las moléculas diatómicas AuH y AgH, realizadas por Pyykkö y mostrados en la figura 4.
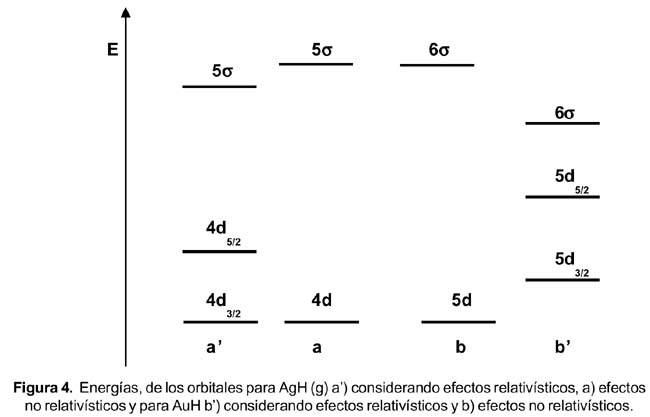
Se puede apreciar que la primera energía de ionización (electrón s) es menor en la plata (5? ) con respecto al oro (6? ). Pero la segunda energía de ionización (electrón que está en d 5/2 ) es menor en el oro que en la plata. Nuevamente, por efectos relativisticos el nivel 6s del oro es mas estable que el de la plata, pero sus orbitales d se desestabilizan más que los de la plata.
Con el oro sucede otro hecho curioso, ¡su afinidad electrónica es de 193 kJ/ mol, que es mayor a la del oxígeno (142,5 kJ/mol)! La razón de esta gran afinidad electrónica es que si el orbital 6s es ocupado por dos electrones el oro adquiere una estabilidad. El oro forma compuestos con otros metales como CsAu en el que el estado de oxidación formal del oro es –1. Por ello, suponer que el oro actúa siempre como un metal electropositivo sería un error.
4. ¿Cuál es la explicación para el efecto del par inerte?
La contracción relativista de los orbitales s significa que para un átomo de elevado número atómico, hay una energía extra de atracción entre los electrones s y del núcleo. Esto se pone de manifiesto en las energías de ionización más elevadas para los electrones 6s, que contribuyen al efecto termodinámico del par inerte 6s.

La configuración electrónica de valencia de los elementos del grupo 13 (B. Al, Ga, In y Tl) es ns 2 np 1 . Estos elementos pueden formar tres enlaces covalentes o, desde otro punto de vista, pueden tener un estado de oxidación formal de +3. Es muy conocido el hecho de que los elementos más pesados de este grupo (y muchos más en el caso del talio) forman muchos compuestos iónicos, con un estado de oxidación formal de +1, en los que sólo se ionizan los electrones del nivel p, pero no los del s. Este comportamiento en la ionización de los elementos más pesados se conoce como efectos del par inerte, relacionado al hecho de que los dos electrones s no se pierden.
Los efectos de apantallamiento y relativísticos son responsables de que todos los elementos del periodo 6 (Tl 6s 2 6p 1 , Pb 6s 2 6p 2 , Po 6s 2 6p 4 ) tengan mayores energías de ionización que sus congéneres del periodo 5 (In, Sn, Te). Por ello, los electrones 6s 2 son reacios a participar en un enlace químico y por ello son estables los estados de oxidación Tl(I), Pb(II) y Bi(III).
Este hecho se puede comprender fácilmente si observamos que el Tl(I) es isoelectrónico al mercurio; su orbital 6s está muy estabilizado en energía y se re-quiere mucha energía para remover los dos electrones de este nivel, aproximadamente 4 848 kJ/mol. Recordemos que para formar un catión se gasta energía que debe ser compensada por la energía reticular y, por otro lado, es muy importante el tamaño del catión, ya que si es grande la energía reticular será menor. En el caso del Tl ambos factores son desfavorables; el alto costo energético de remover los dos electrones 6s y el gran tamaño del Tl(III), hacen que se reduzca mucho la estabilidad de este compuesto iónico. Esta es la razón por la cual existen un gran número de compuesto de Tl(I) y pocos de Tl(III). Sin embargo, se conocen halogenuros de Tl(III) pero su comportamiento es típico de halogenuros covalentes, como cabría esperar.5,6
Blanco plateado
Mercurio vertíendose en una placa de petri
Lo mismo sucede en el caso del plomo (II) que es isoelectrónico al mercurio. El cloruro de plomo (II) forma una red cristalina del tipo iónico. Por otro lado, el cloruro de plomo (IV) muestra enlaces covalentes, aunque es inestable ya que se descompone con la humedad o estalla al calentarlo. Los otros halogenuros de plomo(IV), de bromo y yodo, no existen ya que el potencial rédox de estos halógenos reduce el plomo (IV) a plomo (II).
Adicionalmente al análisis realizado a los electrones 6s 2 , también se podría realizar a los electrones 5s 2 y 4s 2 . Para los electrones 5s 2 el efecto es menor, pero importante y en el caso del 4s 2 es mucho menor el efecto relativístico.
Un caso curioso lo manifiesta el SnCl 2 (5s 2 ) el cual teóricamente es una base de Lewis, pero en presencia de cloruro reacciona para formar [SnCl 3 ] – . Y más aún, los ángulos de enlace ClSnCl de la especie [SnCl 3 ] – son de 90º. Esto último implica que el estaño debe hacer uso de sus orbitales p exclusivamente y no involucran a los s (no se forman orbitales híbridos sp 2 ) ya que deben estar muy estabilizados en energía.3b La vasta cantidad de datos estructurales demuestra que este par de electrones, si bien no participa como una base de Lewis es, muchas veces, estéricamente activo. En términos simplificados, los compuestos del Sn(II) deben tener estructuras regulares si el par libre de electrones permanece en el orbital esférico y simétrico s; pero parece que en muchas moléculas ocurre una mezcla s-p que da a los orbitales del par libre un considerable carácter p (que son direccionables). Ello explica que el SnCl 2 no es lineal (95º), en cambio, en el caso del ZnCl 2 , que no tiene par libre, es de 180º. Además, el [SnCl 3 ] – sí actúa como base de Lewis con BX 3 y con metales de transición.
5. ¿Cómo se explica la contracción lantánida?
Al ir del lantano (Z = 57) al lutecio (Z = 71) se observa que el radio iónico disminuye en 18,3 pm. El llenado electrónico de los orbitales 4f produce una con-tracción gradual, llamada contracción lantánida, no sólo en los radios iónicos sino también en los tamaños atómicos. A medida que se avanza del lantano al lutecio se incrementa la carga nuclear y el número de electrones en el nivel f se incrementa; sin embargo, debido al poco efecto pantalla que brinda un electrón a otro en el nivel f, la carga nuclear efectiva que experimenta cada electrón aumenta, produciéndose una reducción del tamaño de la capa f. Es necesario informar que dicha disminución de tamaño no es muy regular.
Ahora bien, habría que añadir a la explicación ya dada, el efecto relativístico, que contribuye con aproximadamente un 10% a esta contracción. La contracción de los actínidos puede ser explicada en los mismos términos que la de los lantánidos.
Como se ha podido apreciar en esta revisión, los efectos relativísticos pueden explicar una serie de hechos que de otro modo serían un misterio.
DEDICACIÓN
Este trabajo va dedicado a Albert Einstein, ya que habiendo pasado 100 años desde la presentación de cinco trabajos relevantes de Albert Einstein 7 -4 en la revista Annalen der Physik, así como su tesis doctoral- el año 1905 es llamado annus mirabilis de Einstein. Los artículos famosos publicados pueden ser con sultados en las siguientes referencias: Ann. Phys. 1905, Lpz 17 ,132-148, Ann. Phys. 1905, Lpz 17 ,549-560, Ann. Phys., 1905, Lpz 17, 891-921 y Ann. Phys., 1905, Lpz 18, 639-641. En la actualidad se sigue investigando la relatividad aplicada a los elementos y compuestos químicos, los cuales seguro contribuirán a tener una mejor visión y comprensión de la química.
REFERENCIAS
1. P. Pyykkö, Chem. Rev., 1988, 88, 563.
2. L. J. Norrby, J. Chem. Educ., 1991, 68, 110.
3. a) G. Rayner-Canham, “ Química Inorgánica Descriptiva”, Addison Wesley Longman, Segunda edición, México, 2000, p. 30 y 241. b) Ibid, p 288.
4. The University of Hull, http://150.237.140.43/lectures/ajb/non-classical.pdf. (Última vista, 16 de febrero 2005).
5. P. Pyykkö y J-P Desclaux, Acc. Chem. Res., 1979, 12, 276.
6. K. S. Pitzer, Acc. Chem. Res., 1979, 12, 271.
Transcripción de emilio silvera
Sep
26
¡La Física!… tiene tántas historias que…
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)



La mecánica cuántica que conocemos en nuestros días se ha conseguido gracias a la suma de muchos esfuerzos y sería preciso entrar en la historia pasada de esta disciplina que investiga como es el mundo, como funciona la Naturaleza, para saber como se llegó a moldear esos conocimientos que nos llevan al “universo” de lo infinitesimal, de los objetos más pequeños pero que, sin ellos, no podrían existir los más grandes. Ninguna duda nos puede caber ya sobre el hecho cierto de que, la mecánica cuántica, es una de las ramas principales de la Física y está entre uno de los más grandes avances del pasado siglo XX en lo que al conocimiento humano del mundo se refiere. Nos explica el comportamiento de la materia-energía y, de hecho, sin esos conocimientos hubiera sido imposible alcanzar el nivel tecnológico del que hoy podemos disfrutar.
La estructura de las fuerzas familiares como la Gravedad y el magnetismo fueron desarrolladas relativamente temprano. Todos conocemos la historia de Newton y sus trabajos y que, mucho después, dejó perfeccionado Einstein en relación a la fuerza gravitatoria. Las fuerzas electromagnéticas se determinaron también bastante pronto pero, no fue hasta 1927 cuando Dirac realizaría los primeros cálculos cuánticos de interacción de la radiación con la materia y en los años cuarenta y cincuenta gracias a los trabajos de, entre otros, Schwinger y Feynman, se construyó una teoría (electrodinámica cuántica) compatible con los principios básicos de la relatividad y la mecánica cuántica y con una capacidad predictiva asombrosa. Se han conseguido comprender éstos fenómenos, podríamos decir que al nivel de un acuerdo entre los cálculos teóricos y los resultados experimentales de más de diez cifras decimales, y, tal cosa, amigos míos, es un inmenso logro de la mente humana.

No podríamos comprender el macrocosmos sin haber descubierto antes que, en realidad, está fuertemente ligado al microcosmos, a la física subnuclear, ese mundo de lo muy pequeño que, cuando se profundiza en él, nos habla del futuro dinámico del universo y se comienza a ver con claridad como aquellas cuestiones antes no resultas, están ahí, ante nuestros ojos y para que nuestras mentes la puedan entender gracias a la dinámica activa de ese ámbito que resulta ser el campo de las partículas elementales y las fuerzas que con ellas actúan.
Las interacciones débiles y las interacciones fuertes, por su profunda lejanía, tardaron en ser comprendidas. Está claro que, el corto alcance en el que se desarrollan imposibilitaron bastante su hallazgo. Antes, los físicos no tenían acceso al mundo subatómico al que más tarde pudieron entrar de la mano de los microscopios electrónicos, los grandes aceleradores y otros ingenios de increíble alcance y precisición. Así que, a diferencia de lo que pasó con la Gravedad y el electromagnetismo, no se partía de una teoría clásica bien establecida, de manera que se tuvo que construir directamente, una teoría cuántica y relativista de ambas interacciones: la interacción nuclear débil y la interacción nuclear fuerte.

Gerardus ´t Hooft
La empresa de comprender aquellas interacciones fue ardua y se tuvo que esperar hasta los año setenta para encontrar las teorías correctas y completas. En estos años se produjeron, primero la demostración por el holandés Gerard ´t Hooft, culminando los trabajos de su mentor, el también holandés, Martinus Veltman, de la autoconsistencia (llamada, por motivos técnicos, renormalización) de las teorías propuestas fenomenológicamente por Glashow, Wienberg y Salam para interacciones débiles; y segundo, el descubrimiento de la propiedad de libertad asintótica (por Gross, Wilczek y Plotzer) de las interacciones fuertes. Ambos grupos consiguieron el Nobel, pero los tres últimos no vieron premiados sus esfuerzos hasta 30 años después, en 2004, cuando se había comprobado de manera suficiente la veracidad de sus predicciones sobre la libertad de los Quarks en su confinamiento, cuando éstos, están juntos y los Gluones, se comportan como si no estuvieran allí, sólo actúan cuando tratan de separse.

Frank Wilczek (su origen es polaco e italiano) unto con David Groos y David Politzer recibió el Premio Nobel de Física 2004 por el descubrimiento de la libertad asintótica en la teoría de la interacción fuerte.

En 1973, Wilczek, un estudiante graduado trabajando con David Gross en la Universidad de Princeton, descubrió la libertad asintótica que afirma que mientras más próximos estén los quarks menor es la interacción fuerte entre ellos; cuando los quarks están extremadamente próximos la interacción nuclear entre ellos es tan débil que se comportan casi como partículas libres.
Estosd avances hicieron posible obtener teorías consistentes con la relatividad y la mecánica cuántica de ambos tipos de interacciones; teorías que, además han superado con éxito las muchas confrontaciones experimentales que han sido realizadas hasta nuestros días. Aunque no hay ni cálculos teóricos, ni resultados experimentales tan exactos como en el caso de la electrodinámica cuántica, es cierto que el nivel de precisión de los cálculos con interacciones débiles llegan a cuatro y más cifras significativas y, para interacciones fuertes, estamos alcanzando el nivel del uno por ciento.


En ambas imágenes está reflejada la Interacción gravitatoria que, en las grandes estructructuras se hace presente y se deja sentir, podemos ver como funciona y cuáles son sus consecuencia. Sin embargo, en el mundo de lo muy pequeño, esta interacción, continúa siendo la cenicienta en lo que se refiere a la comprensión de la estructura microscópica y la incidencia que la interacción gravitatoria pueda tener ahí y, curiosamente, es la interacción que se conoce desde hace mucho tiempo y sabemos, perfectamente de su funcionamiento en ese ámbito de lo muy grande pero, hace mutis por el foro cuando nos acercamos al mundo de las partículas, de la mecánica cuántica. Por eso se habla tanto de que necesitamos una teoría cuántica de la gravedad.
No tenemos información alguna de la fuerza de Gravedad a nivel experimental sobre la interacción gravitatoria a cortas distancias, donde sólo se puede llegar a través de inmensas energías. A lo más que hemos podido llegar es a experimentos del tipo realizado por Eötvös, midiendo la interacción gravitatoria entre dos cuerpos a distancias del orden del centímetro: las interacciones gravitatorias entre partículas elementales (quarks, electrones o incluso núcleos) es tan minúscula que son pocas las esperanzas de poderlas medir…por ahora ni en muchom tiempo futuro, y, siendo así (que lo es), nos tenemos que dedicar a emitir conjeturas y a especular con lo que podría ser.

En el siglo XIX se consiguió uno e los logros más impresionantes que nunca pudo alcanzar la Humanidad. ¡La comprensión de los fenómenos electromagnéticos. Comprensión en la que participaron (como casi siempre) muchos científicos, entre los que podemos destacar a dos británicos: el inglés Muchael Faraday, responsable de una buena parte de la investigación y de los conceptos experimentales (de él es el concepto de campo que tan importante sería para la Física), y, el escocés James Clerk Maxwell al que le debemos la síntesis teórica que condensó en unas pocas ecuaciones fundamentales, de las propiedades de las interacciones electromagnéticas a nivel clásico, esto es, macroscópico.
Los fenómenos electromagnéticos tal y como se entendían a finales del siglo XIX, se suponían debidos a la fuerza que una carga eléctrica ejerce sobre otra: tanto si las cargas son estáticas (y entonces la fuerza viene dada por la conocida ley de Coulomb) como si están en movimiento, situación en la que se generan campos magnéticos. Las vibraciones de estos campos electromagnéticos se suponían propagándose por el éter (el “éter luminífero”) y la luz se identificaba como un caso particular de estas vibraciones electromagnéticas. La corriente eléctrica se interpretaba como una especie de fluido: recuérdese que, todavía en 1896, Lord Kelvin defendía esta naturaleza continua de la electricidad.


Lo que supuso el descubrimiento de la luz eléctrica para la Humanidad, aunque ahora lo podamos ver como cosa trivial y cotidiana, en realidad vino a cambiar el mundo que se vio de pronto, sacado bruscamente de la penunmbra para sumergirse en la más maravillosa claridad del día artificial. Aquello supuso un cambio enorme para muchos de los ámbitos sociales en las ciudades y, no digamos, más tarde, en el de los hospitales, laboratorios y también en el más cotidiano mundo doméstico.
Está claro que la luz es algo tan importante enn nuestras vidas que, sin ella, nos encontramos desamparados, desnudos y, si nos referimos a la natural, la que nos manda el Sol, la cosa sería más grave ya que, sin ella, no podríamos estar aquí. De todo esto, como de cualquiera de los temas de Física que pudiéramos escoger al azar, nos podríamos estar hablando durante años…¡es tan fascinante! ¡son tan maravillosos! todos esos conocimientos que, de alguna manera, nos acercan a que podamos comprender en funcionamiento del mundo y nos cuentan el por qué ocurren las cosas de la, manera en que la vemos que pasan. Muchas son las historias que se podrían contar de todos estos sucesos que, por el camino de los descubrimientos tuvimos que recorrer.

La teoría cuántica, recordémoslo, afirma que para todo objeto existe una función de onda que mide la probabilidad de encontrar dicho objeto en un cierto punto del espacio y del tiempo. La teoría cuántica afirma también que nunca se conoce realmente el estado de una partícula hasta que se haya hecho una observación. Antes de que haya una medida, la partícula puede estar en uno de entre una diversidad de estados, descritos por la función de onda de Schrödinger. Por consiguiente, antes de que pueda hacerse una observación o medida, no se puede conocer realmente el estado de la partícula. De hecho, la partícula existe en un estado ultramundano, una suma de todos los estados posibles, hasta que se hace una medida.
Cuando esta idea fue propuesta por primera vez por Niels Bohr y Werner Heisemberg, Einstein se revolvió contra ella. “¿Existe la luna sólo porque la mira un ratón?“, le gustaba preguntar. Según la teoría cuántica, en su más estricta interpretación, la Luna, antes de que sea observada, no existe realmente tal como la conocemos. “La Luna puede estar, de hecho, en uno cualquiera de entre un número infinito de estados, incluyendo el estado de estar en el cielo, de estar explotando, o de no estar allí en absoluto. Es el proceso de medida que consiste en mirarla el que decide que la Luna está girando realmente alrededor de la Tierra“. Decía Einstein con ironía.

Einstein no pensó en la posibilidad de que fuera la Luna la que nos esté mirando
Edwin Schrödinger, autor de la ecuación con su función de onda, se disgustó con estas interpretaciones de su ecuación. Para demostrar lo absurdo de la situación creada, Schrödinger colocó un gato imaginario en una caja cerrada. El gato estaba frente a una pistola, que está conectada a un contador Geiger, que a su vez está conectado a un fragmento de uranio. El átomo de uranio es inestable y sufrirá una desintegración radiactiva. Si se desintegra un núcleo de uranio, será detectado por el contador Geiger que entonces disparará la pistola, cuya bala matará al gato.

Para decidir si el gato está vivo o muerto, debemos abrir la caja y observar al gato. Sin embargo, ¿cuál es el estado del gato antes de que abramos la caja? Según la teoría cuántica, sólo podemos afirmar que el gato está descrito por una función de onda que describe la suma de un gato muerto y un gato vivo.
Para Schrödinger, la idea de pensar en gatos que no están ni muertos ni vivos era el colmo del absurdo, pero la confirmación experimental de la mecánica cuántica nos lleva inevitablemente a esta conclusión. Hasta el momento, todos los experimentos han verificado, favorablemente, la teoría cuántica.
La paradoja del gato de Schrödinger es tan extraña que uno recuerda a menudo la reacción de Alicia al ver desaparecer el gato de Cheshire en el centro del cuento de Lewis Carroll: “Allí me verás“, dijo el Gato, y desapareció, lo que no sorprendió a Alicia que ya estaba acostumbrada a observar cosas extrañas en aquel lugar fantástico. Igualmente, los físicos durante años se han acostumbrados a ver cosas “extrañas” en la mecánica cuántica.

La Mecánica cuántica, es , más fascinante el el Pais de las Maravillas de Alicia
Existen varias maneras de abordar esta dificultad de lo incomprensible en mecánica cuántica. En primer lugar, podemos suponer que Dios existe. Puesto que todas las “observaciones” implican un observador, entonces debe haber alguna “conciencia” en el universo. Algunos físicos como el premio Nobel Eugene Wigner, han insistido en que la teoría cuántica prueba la existencia de algún tipo de conciencia cósmica universal.
La segunda forma de tratar la paradoja es la preferida por la gran mayoría de los físicos en activo: ignorar el problema.
El físico Richard Feynman dijo en cierta ocasión: “Creo que es justo decir que nadie comprende la mecánica cuántica. No siga diciéndose a sí mismo, si puede evitarlo, “¿pero cómo puede ser así?” porque usted se meterá “hasta el fondo” en un callejón sin salida del que nadie ha escapado. Nadie sabe como puede ser eso“. De hecho, a menudo se ha dicho que de todas las teorías propuestas en el siglo XX, la más absurda es la teoría cuántica. Algunos dicen que la única cosa que la teoría tiene a su favor es que “es indudablemente correcta”.
¿Siempre será parte del misterio?
Sin embargo, existe una tercera forma de tratar esta paradoja, denominada teoría de los muchos universos. Esta teoría (como el principio antrópico) no gozó de mucho favor en la última década, pero está siendo revitalizada por la función de onda del universo de Stephen Hawking.
Pero, bueno… ¿cómo he llegado hasta aquí? Es cierto que, los senderos de la Física te pueden llevar a tántos sitios…
emilio silvera
















 Totales: 83.924.748
Totales: 83.924.748 Conectados: 41
Conectados: 41

























