Mar
5
El Vacío superconductor: La máquina de Higgs Kibble
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

Resulta que el vacío está lleno a rebosar de partículas virtuales y…
Por su parte, el científico británico Peter Higgs, de 80 años, que dio su nombre a la llamada “partícula divina” en 1964, afirmó que cree que su Bosón seríaá hallado gracias al Gran Colisionador. “Creo que es bastante probable” dijo pocas horas después de que entrara en funcionamiento el gigantesco acelerador. Y, según parece, se está saliendo con la suya.
De todas las maneras, estaría bien saber, a ciencia cierta, cómo es el campo de Higgs del que toman la masa todas las partículas, y conocer, mediante que sistema se transfieren la masa, o, si cuando las partículas entran en el campo de Higgs e interracionan con él, es el efecto frenado el que les otorga la masa.
Claro que, esa, como otras conjeturas sobre los Océanos de Higgs y su dichosa Partícula “repartidora de masa”, no son más que conjeturas que, más adelante, debemos ir comprobando para poder escribirlas con letras de oro en el Libro de la Física, o, por el contrario, desecharlas como se ha hecho con tántas otras ideas y teorías frustradas que nunca llegaron a ninguna parte.
¡Los fotones de Yang-Mills adquieren su masa y el proncipio gauge se sigue cimpliendo! Al principio esta visión no mereció la atención que merecía. Por una parte, la gente penso que el modelo era feo. El principio gauge estaba ahí, pero ya no era el tema central. El “Campo de Higgs” había sido puesto ahí “a propósito” y la “partícula de Higgs”, en sí misma, no era una “partícula gauge”. Si se admitía esto, ¿por qué no introducir más partículas y campos arbitrarios? Estas ideas se consideraron como simples modelos con los que jugart, sin mucho significado fundamental al que ahora se quiere llegar con el LHC pretendiendo hacer bueno todo aquello y, al menos los físicos, insisten en que, el campo y la partícula están ahí…¡ya veremos en qué queda todo esto! Son muchos los cabos sueltos y las cosas sin explicar.
En segundo lugar estaba lo que se llamó “teorema de Goldstone”. Ya se habían priducido antes modelos de partículas con “rotura espontánea de simetría”, pero para la mayoría de esos modelos, Jeoffrey Goldstone habia probado que siempre contenían partículas sin masa y sin espín. Muchos investigadores, por lo tanto, pensaron que la teoría de Higgs también debía contener esa partícula de Goldstone, sin masa y que esto era un inconveniente porque entre las partículas conocidas no había ninguna partícula de Goldstone. Incluso el propio Goldstone había advertido que el Modelo de Higgs no satisfaccía las condiciones para su demostración, así que no tenía que ser válido para este caso, pero todo el mundo estaba tan impresionado con las matemáticas del teorema que el Modelo de Huggs-Kibble no tuvo éxito durante mucho tiempo.
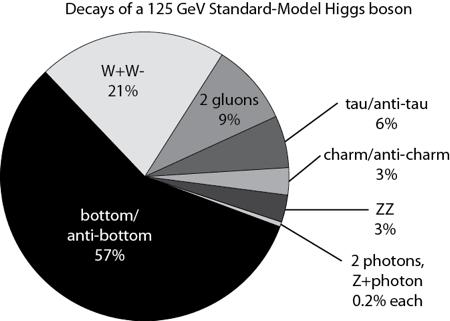
El bosón de Higgs pretende ser una parte integral de nuestra comprensión de la Naturaleza. Se trata de una partícula que es una excitación de lo que se llama el campo de Higgs. El campo de Higgs impregna todo el espacio y cuando algunas de las partículas fundamentales que viajan a través de este campo adquieren masa (al interaccionar con el Campo dónde, probablemente, ve frenada su marcha y su desplazamiento es más lento debido al medio por el que discurre su viaje). La cantidad de masa que adquieren depende de la fuerza en que interactúan con el campo de Higgs. Algunas particulas, como el electrón adquieren una pequeña masa, mientras que otras adquieren una masa mucho mayor.
Y así, el teorema de Goldstone se utilizó como un “teorema de imposibilidad”: si el espacio vacío no es simétrico, entonces no se puede evitar la presencia de partículas sin masa y sin espín. Ahora sabemos que, en nuestro caso, la letra pequeña invalida el teorema; las partículas de Goldstone se hacen incisibles debido a la invariancia gauge y no son más que las “partículas fantasmas” que encontró Feynman en sus cáculos. Además, debemos recordar que el Mecanismo Higgs no es una auténtica rotura de simetría.
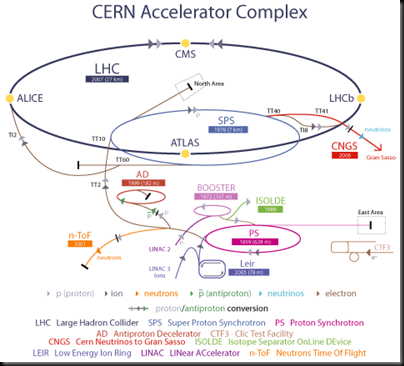
Ingenios que quieren entrar en los campos de Higgs
Un aspecto peculiar de esto es que este campo de Higgs que impregna en todo el espacio es parte de lo que llamamos espacio vacío o el vacío. Es sólo su impacto sobre las partículas que viajan a través de él y el bosón de Higgs que podemos observar en el laboratorio. El bosón de Higgs vive por un lapso muy corto de tiempo, así que no lo observan directamente, sino que más bien se observa que las partículas se descompone en y tienen que inferir su existencia a partir de eso. En la teoría actual que tenemos para comprender la naturaleza podemos hacer afirmaciones precisas acerca de qué fracción del tiempo que se desintegra en dos fotones en comparación con dos quarks abajo.
Claro que, algunos, me piden más profundidad en las explicaciones y, no se conforman con pasar por encima de las cuestiones, hay que entrar más en materia y dejar sentados algunos de los parámetros maemáticos que en todo esto están presente, y, para ellos…
Los físicos han buscado al bosón de Higgs por cerca de 50 años porque su descubrimiento completaría el Modelo Estándar de la física de partículas. El bosón de Higgs y su campo asociado explican cómo la simetría electrodébil se rompió justo después del Big Bang, lo que le dio a ciertas partículas elementales la propiedad de la masa. Sin embargo del Modelo Estándar no predice la masa de Higgs, y varios programas experimentales en el LEP del CERN, en el Tevatron de Fermilab y ahora el LHC del CERN habían intentado medir la masa de la partícula.
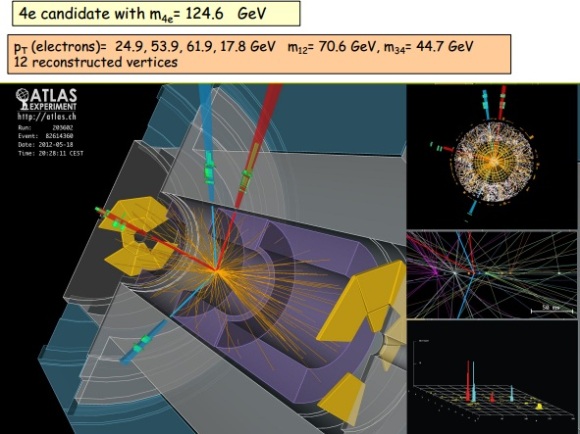
En el seminario llevado a cabo hoy en CERN como preludio a la mayor conferencia de física de partículas de este año, el ICHEP2012 en Melbourne, los experimentos ATLAS y CMS presentaron sus resultados preliminares en la búsqueda del Bosón de Higgs. Ambos experimentos observaron una nueva partícula en la región de masa entre 125-126 GeV.
“Observamos en nuestros datos claras señales de una nueva partícula, al nivel de 5 sigma, en la región de masa alrededor de 126 GeV. El impresionante rendimiento del LHC y ATLAS y el gran esfuerzo de mucha gente nos trajo a esta excitante etapa”, dijo la presentadora del experimento ATLAS Fabiola Gianotti, “pero se necesita más tiempo para preparar estos resultados para su publicación”
“Los resultados son preliminares pero la señal 5 sigma alrededor de 125 Gev que estamos viendo es dramática. Ésta es de hecho una nueva partícula. Sabemos que tiene que ser un bosón y es el bosón más pesado que hemos encontrado hasta ahora,” dijo el presentador del experimento CMS Joe Incandela. “Las implicaciones son muy significantes y es precisamente por esta razón que debemos ser extremadamente diligentes en todos nuestros estudios.”

¿Donde aparece el Higgs en todo esto?
Pues pasemos a hablar de teoría cuántica de campos, en ese tendremos unas densidades lagrangianas que dependerán del campo de cada partícula, dependiendo de su spin será un lagrangiano o otro, por ejemplo para N (a = 1,….N) campos escalares(omito fórmula).
.Al buscar el mínimo del potencial (en realidad un extremal de la acción, pero para lo que nos interesa a nosotros serán mínimos) resulta que hay varios posibles (con el mismo valor) pero para que la energía se minimice hace falta fijar un vacío (debido a que el Hamiltoniano depende del potencial y de unos términos positivos que van con las derivadas del campo). Ahora bien, inicialmente nuestra acción podría tener una simetría gauge global, es decir que al efectuar una transformación de un grupo sobre los campos la acción no cambia, al fijar el vacío la simetría se reduce a un subgrupo
y algunos campos obtienen masa (originalmente ninguno tiene masa), pues bien el teorema de Goldstone lo que dice es que
campos se quedan sin masa, estos son los bosones de Goldstone.
¿Y el higgs?
Ya llegamos, en el apartado anterior hemos considerado transformaciones globales, pero por ejemplo en electromagnetismo tenemos transformaciones locales, así que hay que mirar lo que pasa en las transformaciones locales. Lo primero que pasa es que la derivada parcial no preserva los vectores (lo que hemos llamado antes psi igual que pasa en relatividad general, al hacer una transformación que depende de las coordenadas la derivada ya no es covariante, así que hay que buscar una covariante para seguir con lo que sabemos (en este caso la transformación se debe a un grupo gauge arbitrario, que no tiene porque ser el de difeomorfismos como en relatividad general. En este contexto aparecen los campos gauge que jugaran un papel similar al de la conexión en relatividad general y en el caso del electromagnetismo el campo gauge es el potencial electromagnético). Ahora al ser transformaciones locales, aparecen campos gauge que por similitud con el electromagnetismo escribiremos el lagrangiano de Yang-Mills
igual que en el electromagnetismo F depende de los campos gauge, pero debido a que
no es abeliano hay un termino extra que tiene que ver con las constantes de estructura del álgebra de Lie,
. Ahora ya vien lo bueno, aparte del lagrangiano de la partícula también tenemos el de Yang-Mills, resulta que debido a la simetría local:
- Los bosones de Goldstone desaparecen, es decir no son partículas físicas.
campos gauge obtienen masa
Pues eso es el efecto Higgs. Ahora para llegar ya al famoso bosón, en el modelo estandar no se pueden construir terminos de masa para las partículas debido a que no se pueden acoplar adecuadamente para ese propósito los campos de Yang-Mills y las partículas, debido a las simetrías que deben satisfacer (en general el famoso aunque cada campo tendrá una simetría concreta) y ahí es donde entra el bosón de Higgs, ya que el modelo más sencillo para añadir masa es justamente ese, añadir un doblete de campos escalares complejos y al romper la simetría …….. Higgs !!!!
Dos prestigiosos investigadores habñían sugerido de forma independiente que se podían construir modelos realistas dde partículas en los cuales, el sistema de Yang-Mills fuera responsable de la interacción débil y el mecanismo de Higgs-Kibble la causa de su corto alcance. Uno de ellos era el paquistaní Abdus Salam que estaba buscando modelos estéticos de partículas y pensó que la belleza de la idea de Yan-Mills era razón suficiente para intentar construir con ella un modelo de interacción débil. La partícula mediadora de la interacción débil tenía que ser un fotón de Yang-Mills y el mecanismo de Higgs-Kibble la única explicación aceptable para que esta partícula tuviera una cierta cantidad de masa en reposo.

Una simetría puede ser perfecta en el plano de las ecuaciones y resultar rota en el plano de las soluciones. Como decía Weinberg: «Aunque una teoría postule un alto grado de simetría, no es necesario que los estados de las partículas muestren la simetría. Nada me parece tan halagüeño en física como la idea de que una teoría puede tener un alto grado de simetría que se nos oculta en la vida ordinaria».
La teoría que unifica las interacciones electromagnéticas y débil se debe a Glashow, Salam y Weinberg que obtuvieron por ella el Premio Nobel de física de 1979. La dificultad esencial de esta teoría es que los bosones del estado inicial simétrico debían ser de masa nula (masa nula de los bosones de interacción origina una fuerza a gran distancia), mientras que se necesitan bosones intermedios (partículas que originan la fuerza) muy masivos para justificar la interacción débil (corto alcance) . El mecanismo de Higgs, permite resolver esa dificultad, mediante la ruptura espontánea de simetría hace masivos los bosones W y Z (interacción débil) y mantiene nula la masa del fotón (interacción electromagnética).
Los famosos diagramas de Feynaman, nos explican algunos mecanismos de los que se pueden producir (de hecho se producen) en ese misterioso campo de las partículas elementales cuando están presentes en cuertos lugares y se juntas con otros individuos de la especie.
Salam que estaba muy cerca de poder alcanzar la gloria…no llegaba a poder explicar y aplicar las reglas de Feynman y tuvo quer admitir que la teoría parecía estar llena de partículas fantasmas que estaban a punto de estropearlo todo. En estas, llegó el otro investigador, Steven Weinberg, que supo dar un paso más al formular con mucho más detalle un modelo sencillo en el cual indicaba con precisión los campos que existían y cómo podían interactuar. Pero se limitó a los leptones. Weinberg comprendió que, junto al fotón ordinario tenía que haber tres fotones de Yang-Mills pesados::
– Uno cargado positivamente.
– Otro cargado negativamente.
– Otro Neutro.
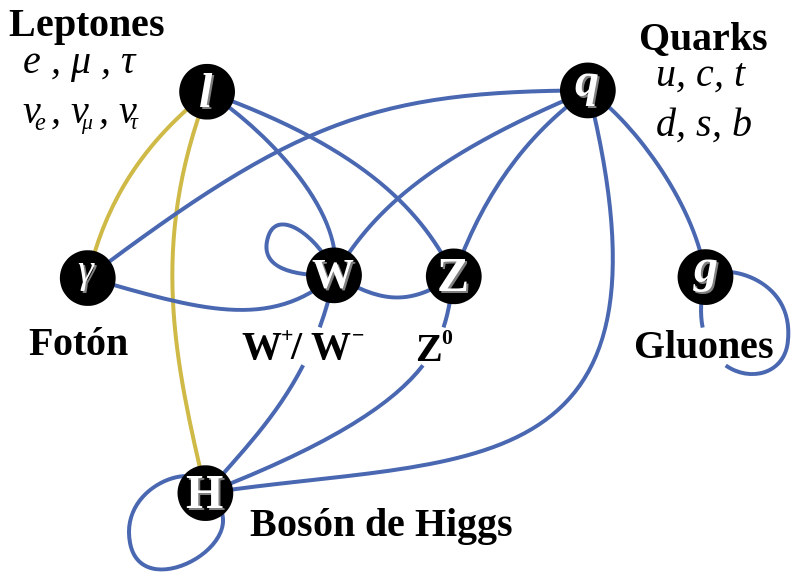
El panorama completo
En lo que se refiere a los fotones cargados, todo el mundo estaba de acuerdo en que estos se necesitarían para describir la interacción débil: serían los famoso bosones vectoriales intermediarios, W+ y W–. De acuierdo con Weinberg, sus masas tenían que ser mayores de 60.000 MeV. Pero solos, estos bosones, vectoriales cargados eran suficientes para explicar todos los procesos de interacción débil que conocían en aquella época. Que aparte de ellos y del fotón ordinario, y, también se necesita otro componente neutro (Weinberg le llamó Zº) no era evidente en absoluto. Se encontró que la masa del Zº tenía que ser un poco mayor que la de los bosones cargados.
De todo aquello surgió una tería para las interacciones débiles en las cuales jugaban un papel dominante distintos diagramas de Feynman, de los que se podían plasmar un número infinito para mostrar, de manera gráfica, los sucesos que acontecían en aquellos fenómenos de la radiación producida en la interacción débil. Pasado el tiempo y mirado con una mejor perspectiva, es fácil comprender todo aquello pero, en aquellos momentos en que se estaba gestando, las cosas no resultaban tan fáciles.

Después de todo aquello, se prestó más atención al mecanismo Higgs-Kibble y, algunos, como Veltman fueron muy escépticos con aquellas ideas, y, desde luego, no fue fácil converlo de que pudiéramos llamar vacío a algo lleno de partículas invisibles. ¿No delatarían dijo, su presencia por sus campos gravitatorios? La teoría puede ser formulada de tal manera que esos campos gravitatorios se compensen exactamente con otras partículas invibles o por una contribución misteriosa del propio espacio vacío.
Cómo consigue la Naturaleza enmascarar tan exacta y eficientemente esos factores de la gravedad que no podemos notar nada, es un misterio que continua siendo muy debatido hoy en día. Claro que, todo esto dejará de ser un misterio cuando un día (lejos aún en el futuro), podamos comprender la Gravedad Cuántica.
Miehntras todo esto sucede… ¡Dejémos volar nuestra imaginación! con ideas y teorías como la de los ¡Campos de Higgs! ¡Bosones que, generosos ellos, regalan masas a otras partículas! ¡Materia que no podemos ver pero que, dem manera acérrima, nos empeñamos en que sí está! ¡Fluctiaciones de vacío que rasgan el espacio-tiempo, y, que de vez en cuando, hace surgir nuevos universos! ¡Universos paralelos que nacieron sin vida! ¡Ciclos eternos en el que las cosas se repetin una y otra vez hasta el infinito! ¡Nuevos Big Bangs después del nuestro! ¡Agujeros negros en nuestro universo y, blancos al otro lado, en otro universo. Aquí recoge materia y, allú, la expulsa por el contrario, un Agujero Blanco! ¡Agujeros de Gusano que nos podrían llevar a otras galaxias! ¡El sueño de vencer (mejor burlar) a la velocidad de la luz, ese muro que nos tiene confinados en nuestro pequeño mundo, el Sistema Solar!
Después de leer todo esto, ¿por qué no dedicais aunque sólo sea una hora para pensar sobre ello?
emilio silvera
Feb
26
¡La Física! ¿Qué haríamos sin ella?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (6)
Comments (6)
Para no viajar muy atrás en el tiempo, fijaremos el punto de partida en 1687, fecha en que salió a la luz la Obra de Newton, sus Principas. El tiempo transcurrió hasta 1900, fecha en la que Planck publicó un artículo de ocho páginas con su idea del cuanto que sería la semilla que daría lugar al nacimiento de la mecánica cuántica. En 1905, aquel joven de la Oficina de Patentes de Berna, sorprendió al mundo de la Física con su Teoría de la Relatividad Especial. Se produjeron muchos desarrollos importantes para nuestras imágenes de la Física Fundamental. Uno de los mayores cambios ocurrido en ese período fue la comprensión, básicamente mediante los trabajos de Faraday y Maxwell en el siglo XIX, de que cierta noción de campo físico, que permea en el espacio, debe cohexistir con la previamente aceptada “realidad newtoniana” de las partículas individuales que interaccionan por medio de fuerzas instantáneas.

Conforme a lo que arriba decimos se producen fenómenos y se ponen en marcha mecanismos que hacen posible que, la imagen que vemos, pueda ser posible gracias a la presencia de fuerzas que, aunque no las podamos ver, su presencia se hace patente por los resultados que en su diversidad, son los mecanismos que llevan el ritmo del universo en el que vivímos.

Más tarde, esta noción de “campo” se convirtió también en un ingrediente crucial de la teoría de la Gravedad en un espaciotiempo curvo a la que llegó Einstein en 1915. Lo que ahora denominamos campos clásicos son el Campo Electromagnético de Maxwell y el Campo Gravitatorio de Einstein.

La presencia del campo gravitatorio de una masa afecta al tiempo y al espacio. La gravedad hace que dos relojes atrasen. Un reloj en la superficie de la Tierra atrasa con respecto a un reloj en la Luna, toda vez que el campo gravitatorio de la Tierra es más potente. De la misma manera, nos podríamos preguntar ¿por qué la gravedad actúa sobre el espacio y alarga el tamaño de los objetos (estirándolos). ¿Dónde podríamos crecer más, si viviéramos en la Tierra o en la Luna?
Pero sigamos. Hoy día sabemos que hay mucho más en la Naturaleza del mundo físico que la sola física clásica. Ya en 1900 -como decimos antes- Max Planck había reveleado los primeros indicios de la necesidad de una “teoría cuántica”, aunque se necesitó un cuarto de siglo más antes de que pudiera ofrecerse una teoría bien formulada y global. También debería quedar claro que, además de todos estos profundos cambios que se han producido en los fundamentos “newtonianos” de la física, ha habido otros desarrollos importantes, tanto previos a dichos cambios como coexistentes con algunos de ellos en forma de poderosos avances matemáticos, dentro de la propia teoría newtoniana.

En 1905 un desconocido Albert Einstein publicaría unos espectaculares estudios sobre la teoría de la relatividad, pero muy pocos científicos, entre ellos Planck, reconocerían inmediatamente la relevancia de esta nueva teoría científica. Tanta fue su importancia que incluso Planck contribuyo a ampliarla.
Pero igualmente, la hipótesis de Einstein sobre la ligereza del quantum (el fotón), basada en el descubrimiento de Philipp Lenard de 1902 sobre el efecto fotoeléctrico fue rechazada por Planck, al igual que la teoría de James Clerk Maxwell sobre la electrodinámica.
En 1910 Einstein desafía la explicación de la física clásica poniendo el ejemplo del comportamiento anómalo del calor específico en bajas temperaturas. Planck y Nernst decidieron organizar la primera Conferencia de Solvay, para clarificar las contradicciones que aparecían en la física. En esta reunión celebrada en Bruselas en 1911, Einstein consiguió convencer a Planck sobre sus investigaciones y sus dudas, lo que hizo forjar una gran amistad entre ambos científicos, y conseguir ser nombrado profesor de física en la universidad de Berlín mientras que Planck fue decano.

Otra área importante de avance sobre la que había que llamar la atención es la termodinámica (y su refinamiento conocido como mecánica estadística). Esta estudia el comportamiento de sistemas de un gran número de cuerpos, donde los detalles de los mocimientos no se consideran importantes y el comportamiento del sistema se describe en términos de promedios de las magnitudes adecuadas. Esta fue una empresa iniciada entre mediados del XIX y principios del XX, y los nombres de Carnot Clausius, Maxwell, Boltzmann, Gibbs y Einstein son los protagonistas.
Termodinámica.- Parte de la física que estudia las relaciones existentes entre los fenómenos dinámicos y los caloríficos. Trata de la transformación de la energía mecánica en calor y del calor en trabajo. También describe y relaciona las propiedades físicas de sistemas macroscópicos de materia y energía. La termodinámica estudia los sistemas que se encuentran en equilibrio. Esto significa que las propiedades del sistema—típicamente la presión, la temperatura, el volumen y la masa— son constantes.
Un concepto esencial de la termodinámica es el de sistema macroscópico, que se define como un conjunto de materia que se puede aislar espacialmente y que coexiste con un entorno infinito e imperturbable. El estado de un sistema macroscópico en equilibrio puede describirse mediante propiedades medibles como la temperatura, la presión o el volumen, que se conocen como variables termodinámicas. Es posible identificar y relacionar entre sí muchas otras variables (como la densidad, el calor específico, la compresibilidad o el coeficiente de expansión térmica), con lo que se obtiene una descripción más completa de un sistema y de su relación con el entorno. Cuando un sistema macroscópico pasa de un estado de equilibrio a otro, se dice que tiene lugar un proceso termodinámico. Las leyes o principios de la termodinámica, descubiertos en el siglo XIX a través de meticulosos experimentos, determinan la naturaleza y los límites de todos los procesos termodinámicos.
¿Cuales son los Principios de la Termodinámica?

Cuando dos sistemas están en equilibrio mutuo, comparten una determinada propiedad. Esta propiedad puede medirse, y se le puede asignar un valor numérico definido. Una consecuencia de ese hecho es el principio cero de la termodinámica, que afirma que si dos sistemas distintos están en equilibrio termodinámico con un tercero, también tienen que estar en equilibrio entre sí. Esta propiedad compartida en el equilibrio es la temperatura. Si uno de estos sistemas se pone en contacto con un entorno infinito situado a una determinada temperatura, el sistema acabará alcanzando el equilibrio termodinámico con su entorno, es decir, llegará a tener la misma temperatura que éste.

Primer Principio.-
La cantidad de calor entregado a un sistema es igual al trabajo realizado por el sistema más la variación de su energía interna. Cuando un sistema se pone en contacto con otro más frío que él, tiene lugar un proceso de igualación de las temperaturas de ambos. Para explicar este fenómeno, los científicos del siglo XVIII conjeturaron que una sustancia que estaba presente en mayor cantidad en el cuerpo de mayor temperatura fluía hacia el cuerpo de menor temperatura. El primer principio es una ley de conservación de la energía. Afirma que, como la energía no puede crearse ni destruirse —dejando a un lado las posteriores ramificaciones de la equivalencia entre masa y energía— la cantidad de energía transferida a un sistema en forma de calor más la cantidad de energía transferida en forma de trabajo sobre el sistema debe ser igual al aumento de la energía interna del sistema. A veces, el primer principio se enuncia como la imposibilidad de la existencia de un móvil perpetuo de primera especie.

Flujo de la energía en los ecosistemas. En los ecosistemas se cumplen pues el primer y segundo principio de la termodinámica.
Segundo Principio.-
El segundo dice que solamente se puede realizar un trabajo mediante el paso del calor de un cuerpo con mayor temperatura a uno que tiene menor temperatura. Al respecto, siempre se observa que el calor pasa espontáneamente de los cuerpos calientes a los fríos hasta quedar a la misma temperatura. La segunda ley afirma que la entropía, o sea, el desorden, de un sistema aislado nunca puede decrecer. Por tanto, cuando un sistema aislado alcanza una configuración de máxima entropía, ya no puede experimentar cambios: ha alcanzado el equilibrio. La naturaleza parece pues ‘preferir’ el desorden y el caos. Puede demostrarse que el segundo principio implica que, si no se realiza trabajo, es imposible transferir calor desde una región de temperatura más baja a una región de temperatura más alta. El segundo principio impone una condición adicional a los procesos termodinámicos. No basta con que se conserve la energía y cumplan así el primer principio. Una máquina que realizara trabajo violando el segundo principio se denomina “móvil perpetuo de segunda especie”, ya que podría obtener energía continuamente de un entorno frío para realizar trabajo en un entorno caliente sin coste alguno. A veces, el segundo principio se formula como una afirmación que descarta la existencia de un móvil perpetuo de segunda especie.
![[espejo.jpg]](http://1.bp.blogspot.com/_RbcHwhHyNUU/ShpFYOgM4zI/AAAAAAAAAYM/_aVI4zFB9pQ/s1600/espejo.jpg)
Tercer principio de termodinámica o principio onfalóscópico, (mirarse el ombligo): La televisión se retroalimenta a sí misma. Se hace televisión para hablar sobre televisión.
Tercer Principio.-
El tercer principio de la termodinámica afirma que el cero absoluto no puede alcanzarse por ningún procedimiento que conste de un número finito de pasos. Es posible acercarse indefinidamente al cero absoluto, pero nunca se puede llegar a él.
Ciclos termodinámicos.-
Todas las relaciones termodinámicas importantes empleadas en ingeniería se derivan del primer y segundo principios de la termodinámica. Resulta útil tratar los procesos termodinámicos basándose en ciclos: procesos que devuelven un sistema a su estado original después de una serie de fases, de manera que todas las variables termodinámicas relevantes vuelven a tomar sus valores originales. En un ciclo completo, la energía interna de un sistema no puede cambiar, puesto que sólo depende de dichas variables. Por tanto, el calor total neto transferido al sistema debe ser igual al trabajo total neto realizado por el sistema. Un motor térmico de eficiencia perfecta realizaría un ciclo ideal en el que todo el calor se convertiría en trabajo mecánico. El científico francés del siglo XIX Sadi Carnot, que concibió un ciclo termodinámico que constituye el ciclo básico de todos los motores térmicos, demostró que no puede existir ese motor perfecto. Cualquier motor térmico pierde parte del calor suministrado. El segundo principio de la termodinámica impone un límite superior a la eficiencia de un motor, límite que siempre es menor del 100%. La eficiencia límite se alcanza en lo que se conoce como ciclo de Carnot.

- Gravitación
- Luz
- Atracción y repulsión eléctricas
- Atracción y repulsión magnéticas
Pero sigamos con el objeto principla de este trabajo del que, como siempre me pasa, me he desviado a la termodinámica que ya se dio hace unos días. Aquí hablamos de los “campos clásicos” y, sobre las teorías físicas de campos de Maxwell y Einstein: la física “clásica” ¿Cómo pudieron hablar y describir a la perfección suscesos que el ojo no podía ver, y, simplemente con la imaginación, lo hicieron posible, hasta tal punto que, cuando hablamos de campos electromagnéticos o gravitatorios, en nuestras mentes se instalan las imágenes de unos y otros que podemos “ver” con toda precisión.
La teoría del electromagnetismo desempeña también un papel importante en la teoría cuántica, pues proporciona el “campo” arquetípico para el desarrollo posterios de la teoría cuántica de campos. Por el contrario, el enfoque cuántico apropiado del campo gravitatorio sigue siendo eninmático, escurridizo y controvertido y, abordar ahora aquí estas complejas cuestiones, seguramente daría lugar a explicaciones farragosas debido a mi ignorancia profunda en esos conocimientos y a la levedad de los que puedo poseer.

Los campos de fuerza de Faraday han dado lugar a que, la imaginación se desboque y corriendo hacia el futuro, haya imaginado inmensas ciudades que, situadas en lugares imposibles, sostienen sin problema a sus habitantes que, resguardados por un “campo de fuerza” están al resguardo de cualquier peligro que del exterior les pueda venir.
Por ahí arriba me refería al hecho de que ya en el siglo XIX se había iniciado un cambio profundo en los fundamentos newtonianos, antes de las revoluciones de la relatividad y la teoría cuántica en el siglo XX. El primer indicio de que sería necesario un cambio semejante se produjo con los maravillosos descubriumientos experimentales de Faraday hacia 1833, y de las representaciones de la realidad que encontró necesarias para acomodar dichos descubrimientos. Básicamente, el cambio fundamental consistió en considerar que las “partículas newtonianas” y las fuerzas” que actúan entre ellas no son los únicos habitantes de nuestro universo.
A partir de ahí había que tomar en serio la idea de un “campo” con una existencia propia incorpórea. Y, fue entonces cuando se produjo la providencial llegada de Maxwell que, al contrario de Faraday, él si entendía bien el complejo mundo de las matemáticas y, en 1864, formuló las ecuaciones que debe satisfacer este “campo” incorpóreo, y quien demostró que estos campos pueden transportar energía de un lugar a otro.

Transportando energía
Las ecuaciones de Maxwell unificaban el comportamiento de los campos eléctricos, los campos magnéticos e incluso la luz, y hoy día son conocidas como las ecuaciones de Maxwell, las primeras entre las ecuaciones de campo relativistas. Desde la perspectiva del siglo XX se han hecho profundos cambios y se ha producido profundos avances en las técnicas matemáticas, las ecuaciones de Maxwell parecen tener una naturalidad y simplicidad concincentes que nos hacen preguntarnos cómo pudo considerarse alguna vez que el campo electromagnético pudiera obedecer a otras leyes. Pero semejante perspectiva ignora el hecho de que fueron las propias ecuaciones de Maxwell las que llevaron a muchos de estos desarrollos matemáticos. Fue la forma de estas ecuaciones la que indujo a Lorentz, Poincaré y Einstein a las transformaciones espaciotemporales de la relatividad especial, que, a su vez, condujeron a la concepción de Minkowaki del espaciotiempo.
¡La Mente Humana! ?Hasta donde podrá llegar? ¿Qué limite tendrá impuesto? La respuesta es sencilla: ¡ No hay límites! Y, aunque dicha afirmación la repita en muchos de mis escritos, esa es la realidad.
emilio silvera
Feb
26
Una reacción nuclear “desafiante”
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
Una nueva clase de reacción de fisión nuclear observada en el CERN ha mostrado importantes puntos débiles en nuestro entendimiento actual del núcleo atómico. La fisión del mercurio-180 se suponía una reacción “simétrica” que daría lugar a dos fragmentos iguales, pero en lugar de ello ha producido dos núcleos con masas bastante diferentes, una reacción “asimétrica” que plantea un serio desafío a los teóricos.

La Ciencia no duerme. En todo el mundo (ahora también fuera de él -en el espacio), son muchos los Científicos que trabajan de manera tenaz para buscar nuevas formas de alcanzar lo ahora inalcanzable y, para ello, se emplean las más sofisticadas estructuras técnicas de avanzados sistemas tecnológicos que hacen posible llegar allí donde nunca nadie había llegado.
Nuevas teorías, nuevos caminos, nuevas investigaciones y, una buena dosis de imaginación que nos llevará hacia mundos imposibles, hacia descubrimientos impensables, hacia la posibilidad de descorrer el velo que esconde muchos de los secretos de la Naturaleza.
Cuanto más secretos podamos desvelar, más cerca estaremos de hacer frente a problemas hoy insolubles y que, el día de mañana, mirando hacia atrás con una sonrisa, podremos recordar como algo del pasado que, una vez superado, nos dio la posibilidad de alcanzar otros niveles más altos, la posibilidad de plantear nuevas preguntas y, la posibilidad de resolver nuevos problemas.
En el artículo que arriba hemos dejado, tenemos un ejemplo de lo poco que sabemos. Muchos creen saber lo que la Materia es, hablan de Gluones y Quarks, de protones y neutrones, de electrones y neutrinos de la Interacción fuerte, electromagnética, débil o de la Gravedad, y, con ello, se sienten muy satisfechos de poseer unos conocimientos profundos que estaban escondidos en las entrañas de la materia misma. Sin embargo, cada día que pasa, cada nueva investigación que realizamos, cada nivel que podemos subir en las energías que empleamos en la Investigación, podemos encontrarnos con asimetrías inesperadas que, de manera violenta nos saquen del error de creer que estamos en posesión de alguna verdad.
En la Ciencia, lo que denominamos “verdad” es efímero, y, lo que hoy puede considerarse como verdad, mañana pasará a ser la mayor de las mentiras. Acordaos de que la Tierra no es el centro de nada, y, que, en verdad, está situada en los suburbios de una Galaxia corriente, alumbrada por un Sol corriente y, seguramente, ocupada por unos seres “corrientes” que (no pondría la mano en el fuego por lo contrario) proliferan por todo el Universo y a los que, más tarde o más temprano, debemos encontrar.
¡La Ciencia! Esa parcela del saber Humano que, al igual que la Lengua y la Escritura, nos diferencia de otros animales que no tuvieron tanta suerte en el reparto.
emilio silvera
Feb
25
¡La Física! y sus personajes
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (6)
Comments (6)
George Gamow
(Odessa, Rusia, 1904 – Boulder, Estados Unidos, 1968) Físico estadounidense de origen ruso conocido por sus trabajos en el campo de la bioquímica y la astrofísica. En 1922 ingresó en la Universidad de Novorossia de su ciudad natal, y al año siguiente pasó a estudiar en la Universidad de Leningrado, centro donde obtuvo la licenciatura en 1926 y el doctorado en 1928. Tras completar su formación en la Universidad de Gotinga, en Copenhague, junto a Niels Bohr, y en Cambridge con Lord Rutherford, fue nombrado profesor de la Universidad de Leningrado, cargo que ejerció entre 1931 y 1933.
Durante esta época, sus investigaciones estuvieron centradas en la física atómica. En el curso 1933-1934 estuvo en el Instituto Pierre Curie de París y como profesor visitante de la Universidad de Londres, después viajó a Estados Unidos invitado como lector por la Universidad de Michigan y, a continuación, fue contratado como profesor de Física por la Universidad George Washington de la capital, puesto en el que permaneció hasta 1956.
Universidad George Washington de Michigan
Ya adquirida la nacionalidad estadounidense, durante los años de la Segunda Guerra Mundial fue llamado por el gobierno, como muchos otros científicos, para trabajar en el proyecto de la bomba atómica. Junto con Ralph Alpher desarrolló una teoría sobre la creación de los elementos químicos, basada en la explosión originaria de un átomo primitivo, conocida popularmente como Big Bang, que Georges Lemaître formuló en 1931 y que él contribuyó a divulgar; asimismo, desarrolló la teoría denominada Gamow-Teller y profundizó en el descubrimiento de Hans Bethe sobre el ciclo que produce la energía estelar.
Fue uno de los primeros científicos en contradecir la idea del enfriamiento del Sol, y en cambio, defender su progresivo calentamiento como posible causa de la extinción de la vida terrestre. En 1954 teorizó sobre la composición del código genético a base de tripletas de nucleótidos, y aunque se equivocó en los cálculos, la idea fue confirmada mediante experimentos en 1961. En 1958 contrajo matrimonio con Barbara Perkins. Desde 1956 fue profesor de Física Teórica en la Universidad de Colorado, y ese mismo año recibió el Premio Kalinga, concedido por la UNESCO por su labor divulgativa de la Ciencia. Sus obras más importantes fueron Un, dos, tres… infinito (1947) y La creación del universo (1952).
George Gamow, el excéntrico físico ruso que (en aquellos tiempos) arriesgí su vida para poder venir a trabajar en América, donde se convirtió en uno de los fundadores de la cosmología moderna e incluso contribuyó a la comprensión inicial de la molécula de ADN y el código genético. Gamow, como todos sus contemporáneos podía ver que había cuatro fuerzas distintas en la Naturaleza (Gravedad, Electromagnétismo y las fuerzas nucleares débil y fuerte). La intensidad de cada una de ellas daría uno de los números puros de Einstein que definen el mundo. Gamow no se veía particularmente atraído por la cuestión de si podía haber sólo un cuarteto de valores posibles. Pero comprender plenamente esos valores -una capacidad de calcularlos o predecirlos de forma precisa- sería para él lo mismo que para un físico el ondear de la bandera de cuadros. Cuando llegara ese día se habría alcanzado una comprensión completa de las fuerzas de la Naturaleza. Gamow se sentía un poco deprimido ante esta perspectiva, comparable a llegar al final de una gran historia o sentarse en la cima de una montaña que uno se ha esforzado en escalar y, al estar allí, preguntarse; ¿Y, ahora qué? ¿Aquí termina todo?

Vayamos hacia atrás en el Tiempo y hablemos un poco de George J. Stoney, el físico irlandés y pensador excéntrico y original al que, en realidad, debemos la forma de deducir si otros planetas del sistema solar poseían o no una atmósfera gaseosa, como la Tierra, calculando si su gravedad superficial era suficientemente intensa para mantener esa atmósfera.
Pero su pasión real estaba reservada a su idea más preciada: el “electrón”. Stoney había deducido que debía existir un componente básico de carga eléctrica. Estudiando los experimentos de Michael Faraday sobre electrolisis, Stoney había predicho incluso cuál debía ser su valor, una predicción posteriormente confirmada por J. J. Thomson, descubridor del electrón en Cambridge en 1.897, dándole la razón a Stoney que finalmente, a esta unidad básica de la electricidad, le dio el nombre de electrón con el símbolo e en 1.891 (antes de su descubrimiento).

Stoney, primo lejano y más viejo del famoso matemático, científico de computación y criptógrafo Alan Turing, también era tío de George Fitzgerald, después famoso por proponer la “contracción Fitzgerald-Lorentz”, un fenómeno que fue entendido finalmente en el contexto de la teoría de la relatividad especial de Einstein.
Stoney, podemos decir con seguridad, fue el primero que señaló el camino para encontrar lo que más tarde conoceríamos como constantes fundamentales, esos parámetros de la física que son invariantes, aunque su entorno se transforme. Ellas, las constantes, continúan inalterables como sucede, por ejemplo, con la velocidad de la luz c, que sea medida en la manera que sea, esté en reposo o esté en movimiento quien la mide o la fuente de donde parte, su velocidad será siempre la misma, 299.792.458 m/s. Algo análogo ocurre con la gravedad, G, que en todas partes mide el mismo parámetro o valor: G = 6’67259 × 10-11 m3 s-2 Kg-1. Es la fuerza de atracción que actúa entre todos los cuerpos y cuya intensidad depende de la masa de los cuerpos y de la distancia entre ellos; la fuerza gravitacional disminuye con el cuadrado de la distancia de acuerdo a la ley de la inversa del cuadrado.

Stoney, profesor de filosofía natural (así llamaban antes a la Física) en el Queen’s College Galway en 1.860, tras su retiro se trasladó a Hornsey, al norte de Londres, y continuó publicando un flujo de artículos en la revista científica de la Royal Dublín Society, siendo difícil encontrar alguna cuestión sobre la que no haya un artículo firmado por él.
Stoney recibió el encargo de hacer una exposición científica del tema que él mismo eligiera para el programa de la reunión de Belfast de la Asociación Británica. Pensando en qué tema elegir, se dio cuenta de que existían medidas y patrones e incluso explicaciones diferentes para unidades que median cosas o distancias o algún fenómeno: se preguntaba la manera de cómo definirlos mejor y como interrelacionarlos. Vio una oportunidad para tratar de simplificar esta vasta confusión de patrones humanos de medida de una manera tal que diese más peso a su hipótesis del electrón.
En tal situación, Stoney centró su trabajo en unidades naturales que transcienden los patrones humanos, así que trabajó en la unidad de carga electrónica (según su concepto), inspirado en los trabajos de Faraday como hemos comentado antes. También, como unidades naturales escogió G y c que responde, como se ha explicado, a la gravedad universal y la velocidad de la luz en el vacío.

En su charla de la Reunión de Belfast, Stoney se refirió al electrón como el “electrino” y dio el primer cálculo de su valor esperado. Demostró que el trío mágico de G, c y e podía combinarse de una manera, y sólo de una, de modo que a partir de ellas se creaban una unidad de masa, una unidad de longitud y una unidad de tiempo. Para la velocidad de la luz utilizó un promedio de las medidas existentes, c = 3 × 108 metros por segundo; para la constante de gravitación de Newton utilizó el valor obtenido por John Herschel, G = 6’67259 × 10-11 m3 s-2 Kg-1, y para la unidad de carga del “electrino” utilizó e = 10-20 amperios. Estas fueron las inusuales nuevas unidades que él encontró, en términos de las constantes e, c y G, y en términos de gramo, metros y segundos:
Mi = (e2/g)½ = 10-17 gramos
Li = ( Ge2/c4) ½ = 10-17 metros
Ti = (Ge2/c6)½ = 3 x 10-16 segundos
Estas son cantidades extraordinarias. Aunque una masa de 10-7 gramos no es demasiado espectacular-es similar a la de una mota de polvo- las unidades de longitud y tiempo de Stoney eran muy diferentes de cualquiera que hubieran encontrado antes los científicos. Eran fantásticamente pequeñas, rosando lo inconcebible. No había (y sigue sin haber) ninguna posibilidad de medir directamente tales longitudes y tiempos.
En cierto modo, esto es lo que se podría haber esperado. Estas unidades no están construidas deliberadamente a partir de dimensiones humanas, por conveniencia humana o para utilidad humana. Están definidas por la propia fábrica de la realidad física que determina la Naturaleza de la luz, la electricidad y la gravedad (c, e y G). No se preocupan de nosotros. Stoney triunfó de un modo brillante en su búsqueda de un sistema de unidades sobrehumanas.

Stoney señaló el camino que más tarde, siguió Planck para elaborar sus unidades y, entre ambos, nos han llevado al Universo de lo infinitesimal que, no por pequeño es menos importante, tanto es así que, estas unidades son las que marcan el límite de nuestras teorías actuales, no podemos ir más allá de su límites. Así resulta ser, por ejemplo con la Teoría M que, necesitando de la energía dee Planck para su verificación, no la tendremos ni ahora ni en muchas generaciones venideras.
La interpretación de las unidades naturales de Stoney-Planck no era en absoluto obvia para los físicos. Aparte de ocasionales comentarios de pasada, sólo a finales de la de´canda de 1960, el estudio renovado de la cosmología llevó a una plena coprensión de estos patrones extraños. Uno de los cuuriosos problemas de la física es que tiene dos teorías hermosamente efectivas -la mecánica cuántica y la relatividad general- pero gobiernan diferentes dominios de la naturaleza.
La una se encarga del micromundo de los átomos y de las partículas elementales. Por el contrario, la relatividad, es siempre necesaria cuando algo viaje a velocidades aluninantes cercanas a c, o, cuando está presente un cuerpo macroscópico que, como las galaxias, influyen en el espacio tiempo para distiorsionarlo y curvarlo. Asó que, con estos resultados, ambas teorías gobiernas “universos diferentes” y, esas fuerzas, no tienen ocasión ni oportunidad de “hablar entre sí” están separadas por distancias que, al parecer, y, al menos hasta el momento, son inalcanzables para ellas.

Hemos hablado de todos esas cuestiones y, de alguna manera, están relacionadas con la transmisión de información. Los límites últimos que podemos esperar para el almacenamiento de la información están impuestos por las constantes de la Naturaleza. Em 1981, un físico israelí, Jacob Bekenstein, hizo una prredicción inusual que estaba inspirada en su estudio de los agujeros negros. Calculó que hay una cantidad máxima de información que puede alnacenarce dentro de cualquier volumen. Esto no debería sorpenedernos, lo que debe´ria hacerlo es que el valor máximo está precisamente determinado por el área de la superficie que rodea al volumen, y no por el propio volumen.
El número máximo de bits de información que puede alnacenarse en un volumen viene dado precisamente por el cómputo de su área supercicial en unidades de Planck, Supongamos que la región esférica. Entonces su área superficieal es precisamente proporcional al cuadrado de su radio, mientras que el área de Planck es proporcional a la longitud e Planck al cuadrado (10-66 x R2. Esto es muchísimo mayor que cualquier capacidad de almnacenamiento de información producida hasta ahora. Asimismo, hay un límite último sobre el ritmo de procesamiento de la información que viene impuesto por las constantes de la Naturaleza, ninguna información se puede tansmitir más rápida que la velocidad de la luz. de Esa manera, de alguna forma, se han unido las dos teorías de la mecánica cuántica y de la relatividad, y, cada una de ellas, impone su criterio en el área que le corresponde mandar.

Todas las estructuras del Universo que se comportan como objetos estables, en realidad, se muestran así como consecuencia de que son, malabarismos que se producen entre dos fuerzas antagónicas equivalentes que consiguen esa “delicada” estabilidad que está centrada en la lucha entre la atracción y la reoulsión. Por ejemplo, en un planeta, como la Tierra, hay un equilibrio entre la fuerza atractiva de la Gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos y se llegan a degenerar por el Principio de exclusión de Pauli quen no permite que dos fermiones ocupen el mismo lugar. Todos esos equilibrios pueden expresarse aproximadamente en términos de los números puros de Stobe-Planck creados a partir de las constantes e, h, c, G y mpr
α = 2πe2/hc = 1/137
αG = Gmpr 2/hc ≈ 10-38
La identificación de constantes de la Naturaleza como α y αG, junto con los números que desempeñam el mismo papel definitorio para las fuerzas débil y fuerte de la Naturaleza, nos anima a pensar por un momento en mundos diferentes al nuestro. Estos otros mundos pueden estar definidos por leyes de la Naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizadas por duiferentes valores de constantes adimensionales. estos cambios numéricos alteran toda la fábrica de los mundos imaginarios. Los equilibrios entre los fuerzas serán diferentes de los que se dan en el nuestro. Los átomos pueden tener propiedades diferentes. La Gravedad podría tener un papel más pequeño en esos otros mundos. La Naturaleza cuántica de la realidad podría intervenir en lugares inimaginables.
Claro que, nosotros, nos tenekos que ceñir a éste, nuestro Universo que nos muestras unas leyes y unas constantes que son como son y no de otra manera y, de esa forma, está construido nuestro universo conocido que, en alguna ocasión he pensado sino tendrá “otro universo” escondido dentro de este mismo.
emilio silvera
Feb
17
¿Hasta dónde llegaremos?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (4)
Comments (4)
La intuición natural y la habilidad experimental de Faraday hicieron avanzar enormemente el estudio de todos los fenómenos electromagnéticos. De él es, precisamente, el concepto de campo que tanto juego ha dado a la física.
Sin embargo, para desarrollar una teoría consistente del electromagnetismo se necesitaba un científico distinto: Faraday era hábil experimentador con enorme intuición, pero no sabía expresar matemáticamente lo que descubría, y se limitaba a contarlo. No hubo que esperar mucho, ni salir de Gran Bretaña para que un científico adecuado, un escocés de nombre James Clerk Maxwell (1.831 – 1.879), hiciera acto de presencia.
Maxwell desarrolló las matemáticas para expresar una teoría del magnetismo-electricidad (o al revés) que sentó las bases físicas de aquel fenómeno y contestaba a todas las preguntas de los dos aspectos de aquella misma cosa, el electromagnetismo. En sus ecuaciones vectoriales estaban todos los experimentos de Faraday, que le escribió una carta pidiéndole que le explicara, con palabras sencillas, aquellos números y letras que no podía entender.
Pero además, Maxwell también contribuyó a la física estadística y fue el primer director del Laboratorio Cavendish, unido de manera indisoluble a la física de los siglos XIX y XX (y también al de biología molecular) con sede en Cambridge.
















 Totales: 83.912.911
Totales: 83.912.911 Conectados: 46
Conectados: 46























