Feb
7
¿La Teoría de Cuerdas? ¿Qué es eso? 2ª Parte
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Teoría de Supercuerdas ~
Clasificado en Teoría de Supercuerdas ~
 Comments (3)
Comments (3)

Ayer, cuando hablaba de la T. de cuerdas, al final decía:
Las amplitudes duales, aunque implementaban la idea de democracia nuclear, daban ineludiblemente lugar a un comportamiento de las amplitudes a altas energías mucho más suave del que se observaba en la realidad. Por otro lado los avances formales habían mostrado que la consistencia de la teoría exigía un espacio tiempo de dimensión 26 y que el espectro contenía al menos un taquión (una partícula con masa imaginaria). Estos defectos fueron pronto, parcialmente subsanados, dando lugar a conceptos que han ocupado un papel crucial en la Física de los últimos lustros; estoy hablando de la supersimetría y al renacimiento de las ideas de Kaluza y Klein sobre espacio-tiempo con más de cuatro dimensiones.
Seguiremos hablando de la Teoría de Cuerdas y llegaremos hasta la actual posición que ocupa ésta compleja idea que algunos físicos han venido desarrollando en los últimos cuarenta años y que, nadie sabe en qué pueda desembocar. Muchas han sido las teorías que han sido desarrolladas y, siempre, nos dieron respuestas a cuestiones que, en un principio, ni podíamos imaginar.

Con la llegada de la QCD (Cromo Dinámica Cuántica) quedó de manifiesto que la democracia nuclear era una ilusión resultado de nuestra ignorancia como tántas veces nos ha pasado a lo largo de la historia de la física y de la astronomía. Las resonancias son objetos compuestos, y la teoría fundamental que describe sus constituyentes no se rige por el principio de democracia nuclaer sino por un principio distinto: el de libertad asintótica.
Lo que este principio nos dice es que la teoría deviene invariante de escala a distancias muy pequeñas, es decir, a altas energías, y que los constituyentes fundamentales son los grados de libertad de esta teoría conforme. Una manera fácil de entender la diferencia entre “democracia” y “libertad” es analizando el comportamiento de las amplitudes de colisión a altas energías.
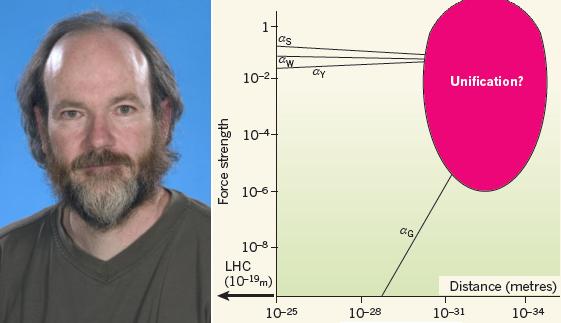
El sueño de Einstein es el sueño de la física teórica moderna: unificar la gravedad con las otras interacciones fundamentales de la naturaleza. Un artículo publicado en Nature estudia cómo se ve afectado el electromagnetismo (una teoría gauge abeliana) debido a la existencia de la gravedad. Las constantes de acoplamiento que caracterizan la “fuerza” de las interacciones fundamentales cambian con la energía. A energías muy altas, o distancias muy cortas, las tres constantes convergen entre sí (de forma aproximada en el modelo estándar y de forma exacta en las teorías supersimétricas). Sin embargo, el comportamiento de la gravedad a distancias ultracortas, en el rango entre 10-32 m y 10-35 m, influye o afecta a las constantes de acoplamiento incluso aunque no se conoce la teoría cuántica correcta de la gravedad, ya que dicha teoría solo es necesaria a distancias menores de 10-35 m. El nuevo análisis indica que el efecto de la gravedad sobre las otras interacciones fundamentales podría ser observado a distancias entre 10-33 m y 10-35 m; en concreto se observaría un cambio en el fenómeno llamado libertad asintótica de las constantes de acoplamiento. La idea ya fue propuesta por Robinson y Wilczek, pero el autor, David J. Toms, va más allá en dicho análisis. Para mí ha sido muy sorprendente encontrar un artículo de física teórica “exótica” en una revista tan poco amante de la teoría “pura” como Nature. Espero que sirva de precedente para futuros análisis. Nos ha comentado el artículo el genial Giovanni Amelino-Camelia, “Fundamental physics: Gravity’s weight on unification,” Nature 468: 40–41, 04 November 2010; el artículo técnico es David John Toms, “Quantum gravitational contributions to quantum electrodynamics,” Nature 468: 56–59, 04 November 2010 [acceso gratis al artículo en ArXiv, 5 oct. 2010]. (De Francis (th)E mule Science’s News).

La Libertad Asintótica nos habla de que las fuerzas entre partículas como los Quarks se hacen más débiles a distancias más cortas (es decir, a altas energías) y se anulan a medida que las distancias entre las partículas tienden a cero. Este fenómeno se puede observar en la fuerza nuclear fuerte, entre los quarks que si se alejan los unos de los otros aumenta la fuerza y, cuando se juntan, esta disminuye.
En una versión democrática basada en la teoría de Cuerdas todos los constituyentes tienen un tamaño mínimo igual al de la longitud L de la cuerda (si estamos tratando con resonancias nucleares esta longitud será del orden de su tamaño, es decir 1/Λ(QCD). Como consecuencia de ello la colisión con transferencias de momento mayores que 1/L deberá estar muy suprimida. Por el contrario, la libertad asintótica predice que a estas pequeñas distancias la teoría deviene esencialmente libre y como consecuencia la amplitud es invariante de escala, presentando un comportamiento característico que se conoce como “scaling” de Bjorken. La constatación experimental de este hecho constituyó el primer deceso de la Teoría de Cuerdas.

(Scaling Bjorken se refiere a una importante simplificación en características ampliación de una gran clase de adimensionales cantidades físicas en partículas elementales, sino que sugiere fuertemente que observados experimentalmente partículas de interacción fuerte (hadrones) se comportan como colecciones de punto-como componentes cuando se probaron a altas energías. Una característica de hadrones probaron en experimentos de dispersión de alta energía se dice que la escala cuando se determina no por la energía absoluta de un experimento, pero por adimensionales cantidades cinemáticas, tales como un ángulo de dispersión o la relación de la energía a una transferencia de momento. Debido a que el aumento de energía implica potencialmente resolución espacial mejorada, escalamiento implica independencia de la escala de resolución favorable, y la subestructura por lo tanto eficaz como un punto. Comportamiento de la escala fue propuesta por primera vez por James Bjorken en 1968 para las funciones de la estructura profunda de dispersión inelástica de electrones en nucleones. Esta idea, junto con el concepto contemporáneo de partons propuestas por Feynman, y el descubrimiento experimental de (aproximadamente) comportamiento de escala, junto inspiró la idea de la libertad asintótica, y la formulación de la cromodinámica cuántica (QCD), la teoría moderna fundamental de las interacciones fuertes.)
Ejemplo de estructura de color de un neutrón. Puede observarse la composición de quarks y la carga de color que adopta.
La QCD no sólo se convirtió en la teoría canónica de dichas formas de interacción, sino también en modelo de Teoría Cuántica de campos, dando lugar a lo que se conoce como el paradigma Wilsoniano de definición de una teoría cuántica relativista como aquella que en el ultravioleta, es decir, a pequeñas distancias, deviene invariante conforme.
Este primer deceso de la Teoría de Cuerdas no fue en absoluto definitivo. La Teoría contenía en su interior secretos que una vez convenientemente entendidos la harían renacer con objetivo muy distinto y mucho más ambicioso: ¡convertirse en el paradigma de la Teoría Cuántica de la Gravedad! ¿Cómo fue eso posible?
¿Dónde estará la verdad?
Lo primero que debemos entender es la inevitabilidad de la gravitación en la Teoría de Cuerdas. Una vez conjugamos efectos cuánticos con el carácter extenso de la cuerda aparece inevitablemente en el espectro un gravitón, y es esta inevitabilidad de la gravitación la que nos aporta una comprensión nueva de la escala de longitud de la cuerda. En breves palabras, si parametrizamos por g la amplitud cuántica de que una cuerda se divida en dos y por L la escala de longitud de la misma, nos encontramos conque gL es precisamente la longitud de Planck:

Dicho de otra manera, la constante de Newton G, que define la intensidad gravitatoria, ¡es simplemente (gL)! Y, este hecho, tiene importantísimas consecuencias. En efecto, si la longitud de Planck está definida de manera intrínseca, podemos asociar, sin salirnos de la propia teoría, con cualquier modo de vibración de la cuerda de masa M su radio gravitacional, o, si se prefiere, su tamaño gravitatorio: R(M) = MG. Una vez hacemos esto aparece de manera inmediata una masa o energía crítica por encima de la cual el modo de vibración de la cuerda adquiere un tamaño gravitacional mayor que su propia longitud.

Este modo de vibración se ha convertido en ¡un agujero negro! Dicho con otras palabras, cuando profundizamos en el ultravioleta llega un momento en el que las excitaciones de la cuerda no nos desvelan una estructura de constituyentes más elementales sino algo completamente nuevo, a saber: agujeros negros cuyo tamaño en vez de disminuir con la energía aumenta. El paradigma de teoría cuántica de campos Wilsoniana caracterizado por la libertad asintótica, en suma por unos constituyentes casi libres, se transforma, en la Teoría de Cuerdas, en una oscuridad asintótica controlada por agujeros negros. En otras palabras, la cuerda, de manera inevitable, se completa en el ultravioleta gravitacionalmente sin desvelar una subestructura Wilsoniana de constituyentes más fundamentales regidos por alguna teoría conforme.

Es importante que apreciemos que la manera en la que la teoría se completa en el ultravioleta no es en término de un espectro nuevo, como podrían ser los quarks y gluones en el caso de la QCD, sino en término de objetos, como son los agujeros negros, cuya definición no nos exige en ningún momento invocar nuevos grados de libertad, sino tan solo la propia dinámica de la teoría.
Así, la Teoría de Cuerdas es una teoría cuántica cuya física en el ultravioleta profundo, a distancias más pequeñas que la propia longitud de la cuerda, está dominada por agujeros negros clásicos. ¿Cómo derivar estos comentarios a un principio rector y definitorio de la Teoría?

No, la potencia utilizada en estas colisiones, no dejan ver las cuerdas que, están mucho más allá de las energías que ahora podemos utilizar
Hay que conseguir que se puedan hacer consistentes los principios de la Mecánica Cuántica con nuevos postulados: el de la existencia de una longitud mínima. Cuando intentamos combinar estos dos principios de una manera consistente nos encontramos con una teoría en el ultravioleta, es decir, más allá de la longitud mínima, debe poder ser descrita no en términos de constituyentes más primitivos sino necesariamente en términos de configuraciones o entidades de la propia teoría cuyo tamaño efectivo es necesariamente mayor que la longitud mínima. Esta descripción “infrarroja” (grandes distancias) del mundo ultravioleta es lo que se conoce como correspondencia UV/IR y es el corazón de la celebradísima e importantísima correspondencia descubierta hace ya más de diez años por Juan Maldacena.
Juan Maldacena ha realizado importantes avances relacionados con la teoría de cuerdas, un marco de unificación teórica de los dos grandes pilares de la física contemporánea: la mecánica cuántica y la teoría de la relatividad general, de Einstein. Maldacena ha propuesto una relación sorprendente entre dos sistemas aparentemente diferentes:
- La teoría de cuerdas IIB propagándose en un espacio-tiempo con una geometría dada por el producto de un espacio anti de Sitter 5-dimensional y una 5-esfera.
- Una teoría cuántica de campos en 4 dimensiones con simetría gauge SU(N) y supersimetría N=4.
Su descubrimiento es conocido como “la conjetura de Maldacena”, la “correspondencia AdS/CFT” o la “correspondencia gauge/cuerda”. Se trata de una relación explícita del principio holográfico (de ´t Hooft y Susskind), que relaciona una teoría con interacciones gravitacionales con una teoría sin gravedad y en un número menor de dimensiones. Tiene profundas implicaciones para el estudio de la gravedad cuántica. Por ejemplo, la correspondencia permite en principio estudiar la descripción microscópica y la dinámica de un agujero negro, y el problema de la pérdida de información en agujeros negros, utilizando el punto de vista dual de un proceso en una teoría cuántica de campos. Esto implica automáticamente que la formación y evaporación de agujeros negros es un proceso descrito de forma unitaria en mecánica cuántica, y que la información no se pierde al caer a un agujero negro. Por otro lado, la correspondencia tiene también aplicación al estudio de fenómenos de interacción fuerte en teorías gauge mediante el dual gravitacional. De hecho, el uso de técnicas basadas en la correspondencia AdS/CFT han supuesto nuevos puntos de vista sobre problemas de QCD como el del confinamiento, y están encontrando aplicación en el análisis de las propiedades del plasma de quarks-gluones, experimentalmente obtenido en el experimento RHIC.
La propuesta de esta correspondencia por parte de Maldacena, y su amplia y profunda investigación sobre sus diversas ramificaciones, le han significado un reconocimiento mundial de la comunidad científica.


Lo cierto es, amigos míos que, entre unos pensadores y otros, vamos acercándonos más y más al saber del mundo. Hemos desvelado importantes secdretos del mundo mágico de las galaxias en el Universo, y, posiblemente, habiendo podido desvelar también, ese otro “mundo” no menos maravilloso de lo muy pequeño donde se encuentra el ámbito de los átomos, no podemos dudar de que, en el futuro, también sabremos llegar a esas cuerdas vibrantes que, de ser cierto que están ahí, nosotros las podremos encontrar, toda vez que, como tenenmos más que demostrado, imaginación no nos falta.
Para finalizar el trabajo de César Gómez, en el que se pregunta qué es la teoría de cuerdas, habrá que cerar con sus mismas palabras:
“De esta forma alcanzamos lo que podría ser una primera definición de la Teoría de Cuerdas: una teoría cuántica con una longitud fundamental mínima. Pero para entender el siggnificado profundo de esta definición deberemos aproximarnos a ella como lo hacemos cuando Einstein nos desveló que la teoría de la Relatividad es una cinemática con una velocidad fundamental máxima. Lo esencial no es entender desde una perspectiva galileana -sobre la base de complicados modelos de éter- cómo es que la de la luz puede ser la velocidad máxima. Lo crucial es postular que es máxima y acomodar la Cinemática y el propio espacio-tiempo a este postulado.

Ciertamente creo que existe un mínimo para todo:
Existe una unidad mínima de tiempo posible, y es o,0000000000000000000000000000000000000000001 seg. Bueno, lo que se conoce como Tiempo de Planck. Sus Unidades, las unidades de Planck, son las que marcan el límite de nuestras teorías, nunca nadie, ha podido sobrepasar lo que miden esas unidades de espacio, masa, tiempo…
Así, continúa diciendo César, al decir que hay una longitud mínima no se trata de explicar desde una perspectiva Wilsoniana cómo surge esta escala o por qué es mínima, sino postular la existencia de una longitud mínima y deducir de ello un paradigma no Wilsoniano de Teoría Cuántica. Y es esto lo que la Teoría de Cuerdas intenta conseguir desde su primer deceso.
Quizás la clave última de la respuesta es que la propia Longitud de Planck es una longitud mínima e intentar entender esta afirmación como un postulado en pie de igualdad con el postulado relativista sobre la imposibilidad de una velocidad mayor a la de la velocidad de la luz en el vacío. “La Velocidad de la Luz y la Longitud de Planck, definen cotas en la teoría de la información; en un caso a la velocidad de transmisión y en el otro a la capacidad de almacenamiento.”
Lo cierto es que, la primera expresión de las TC’s fue desarrollada por Jöel Scherk, de París, y John Schwuarz, del Instituto de Tecnología de California, quienes en el año 1974 publicaron un artículo en el que demostraban que la TC podía describir la fuerza gravitatoria, pero sólo si la tensión en la cuerda se tensiometrara alrededor de un trillón de toneladas métricas. Las predicciones de la teoría de cuerdas serían las mismas que las de la relatividad general a escala de longitudes normales, pero diferirían a distancias muy pequeñas, menores que una trillonésima de un cm. Claro está, que en esos años, no recibieron mucha atención por su trabajo.

Ahora se buscan indicios de la teoría de cuerdas en los grandes aceleradores de partículas donde parece que algunos indicios nos dicen que se va por el buen camino, sin embargo, nuestros aceleradores más potentes necesitarían multiplicar por un número muy elevado su potencia para poder, comprobar la existencia de las cuerda situadas a una distancia de 10-35 m, lugar al que nos será imposible llegar en muchas generaciones. Sin embargo, en las pruebas que podemos llevar a cabo en la actualidad, aparecen indicios de una partlicula de espín 2 que todos asocian con el esquivo Gravitón, y, tal indicio, nos lleva a pensar que, en la teoría de supercuerdad, está implícita una Teoría Cuántica de la Gravedad.
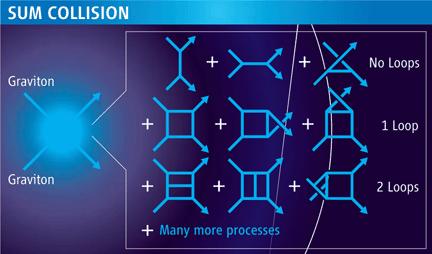
Bueno, buscamos las cuerdas y aún, no henmos encontrado el Gravitón
Los motivos que tuvo la comunidad científica, entonces, para no brindarle la suficiente atención al trabajo de Scherk y Schwuarz, es que, en esos años, se consideraba más viable para describir a la interacción fuerte a la teoría basada en los quarks y los gluones, que parecía ajustarse mucho mejor a las observaciones. Desafortunadamente, Scherk murió en circunstancias trágicas (padecía diabetes y sufrió un coma mientras se encontraba solo en su estudio). Así, Schwuarz se quedó solo, en la defensa de la teoría de cuerdas, pero ahora con un valor tensiométrico de las cuerdas mucho más elevado.
Pero con los quarks, gluones y también los leptones, en la consecución que se buscaba, los físicos entraron en un cuello de botella. Los quarks resultaron muy numerosos y los leptones mantuvieron su número e independencia existencial, con lo cual seguimos con un número sustancialmente alto de partículas elementales (60), lo que hace que la pregunta ¿son estos los objetos más básicos?
Los físicos creen que no, que son las cuerdas vibrantes los objetos más pequeños que componen la materia. Claro que, del dicjho al hecho… ¡va un largo, largo, largo, muy largo trecho!
emilio silvera
















 Totales: 67.074.255
Totales: 67.074.255 Conectados: 47
Conectados: 47